% subspace method
[thetas,residues]=sm(R,A,B,2);
arrowb(thetas,residues); hold on;
Ac=compan(eye(1,6));
Bc=eye(5,1);
That=dlsim_complex(Ac,Bc,y');
[th_esprit,r_esprit]=sm(That,Ac,Bc,2); % ESPRIT spectral lines
arrowg(th_esprit,r_esprit);
Subspace methods
We start with the Carath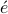 odory-Fej
odory-Fej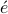 r-Pisarenko result for Toeplitz matrices. Given a
r-Pisarenko result for Toeplitz matrices. Given a 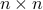 positive definite
Toeplitz matrix
positive definite
Toeplitz matrix 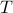 ,
let
,
let 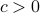 be the smallest number such that
be the smallest number such that 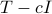 is singular and has rank
is singular and has rank 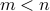 , then
, then
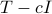 has the formE
has the formE
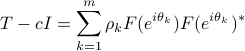
where
![F(e^{itheta_k})= left[ begin{array}{c} 1 e^{itheta_k} vdots e^{i(n-1)theta_k} end{array} right].](eqs/1272814962-130.png)
Accordingly, the power spectrum 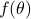 deomposes as
deomposes as
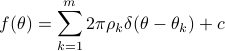
where 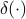 is the Dirac function. The decomposition corresponds to a set of white noise. See MA decomposition for a decomposition corresponds moving-average (MA) noise.
is the Dirac function. The decomposition corresponds to a set of white noise. See MA decomposition for a decomposition corresponds moving-average (MA) noise.
The above result can be generalized to the case of state covariances [1].
More specifically, let 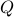 be the unique solution to the Lyapunov equation
be the unique solution to the Lyapunov equation
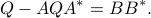
The matrix 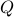 is the state covariance when the input is pure white noise. Let now
is the state covariance when the input is pure white noise. Let now 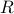 be an arbitray state covariance, let
be an arbitray state covariance, let  be the smallest eigenvalues of the matrix pencil
be the smallest eigenvalues of the matrix pencil 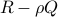 , and assme that the rank of
, and assme that the rank of 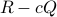 is
is 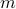 , then
, then
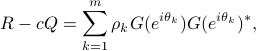
where 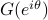 is generalization of
is generalization of 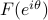 .
.
The subspace spectral analysis methods rely on the singular value decomposition
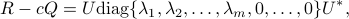
where 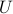 is a unitary matrix and
is a unitary matrix and 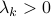 ,
, 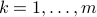 . Partition
. Partition
![U=[U_{1:m},; U_{m+1:n}]](eqs/272044314-130.png)
where 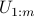 and
and 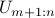 are the first
are the first 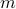 and the last
and the last 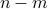 columns of
columns of 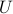 , respectively.
Based on this decomposition, there are two ways we can proceed generalizing the MUSIC and ESPRIT methods, respectively [P. Stoica, R.L. Moses, 1997].
, respectively.
Based on this decomposition, there are two ways we can proceed generalizing the MUSIC and ESPRIT methods, respectively [P. Stoica, R.L. Moses, 1997].
Noise subspace analysis
The columns of 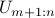 span the null space of
span the null space of 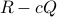 , while the signal
, while the signal 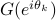 ,
,  is in the span of the columns of
is in the span of the columns of 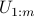 .
So the nonnegative trigonometric polynomial
.
So the nonnegative trigonometric polynomial
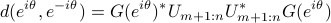
has 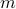 roots at
roots at 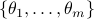 .
.
Given a sample state covariance matrix 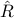 and an estimate on the number of signals
and an estimate on the number of signals 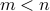 , we let
, we let 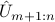 be the matrix of singular vectors of the smallest singular values, and
be the matrix of singular vectors of the smallest singular values, and 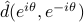 be
the corresponding trigonometric polynomial for
be
the corresponding trigonometric polynomial for 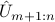 . Two possible generalization of the MUSIC method are as follows.
. Two possible generalization of the MUSIC method are as follows.
Spectral MUSIC: identify
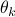 , for
, for 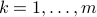 as the values on
as the values on ![[-pi,; pi]](eqs/481304345-130.png) where
where
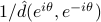 achieves the
achieves the 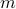 -highest local maxima.
-highest local maxima.Root MUSIC: identify
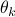 , for
, for 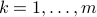 as the angle of the
as the angle of the 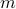 -roots of
-roots of 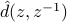 which have amplitude
which have amplitude 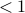 and are closest to unit circle.
and are closest to unit circle.
Signal subspace analysis
A signal subspace method relies on the fact that for the pair 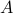 ,
, 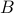 and
and 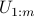 given above, there is a unique solution to the following matrix equation
given above, there is a unique solution to the following matrix equation
![U_{1:m} =[B ~ AU_{1:m}] left[begin{array}{c}muPhi end{array} right],](eqs/1198537117-130.png)
where 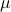 is
is 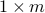 row vector and
row vector and 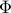 a
a 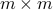 matrix. The eigenvalues of
matrix. The eigenvalues of 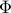 are
precisely
are
precisely 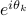 for
for 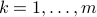 .
If
.
If 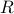 is a Toeplitz matrix and
is a Toeplitz matrix and 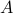 ,
, 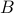 given as in
given as in 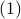 with
with 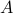 a companion matrix, then we
recover the ESPRIT result [P. Stoica, R.L. Moses, 1997].
a companion matrix, then we
recover the ESPRIT result [P. Stoica, R.L. Moses, 1997].
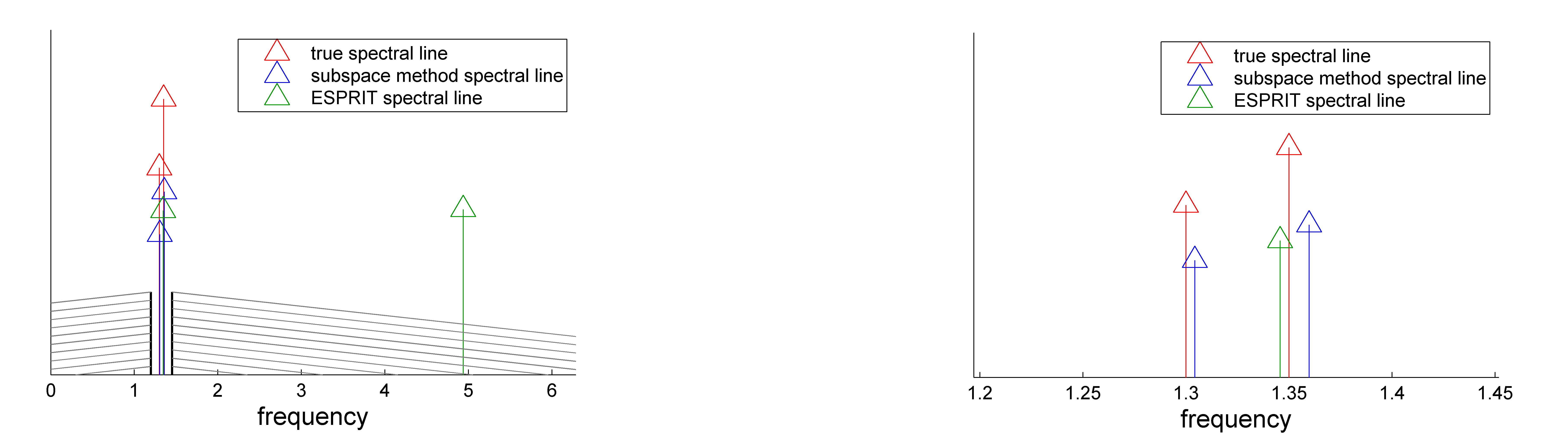
The signal subspace estimation computed using sm.m, whereas music.m and esprit.m implement the MUSIC and ESPRIT methods, respectively. For the example discussed above, the estimated spectral lines are shown in the following figure. For an extensive comparison of the high resolution method sm.m with MUSIC and ESPRIT methods, see the example.
 |