% spectral envelop
rhohalf = envlp(R,A,B,th);
rho = rhohalf.^2;
plot(th,rho);
Spectral envelop
Let 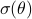 denote a spectral measure of the stochastic process
denote a spectral measure of the stochastic process  , the envelop of maximal spectral power is defined as
, the envelop of maximal spectral power is defined as
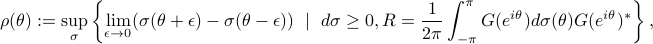
where 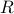 represents the state covariance and
represents the state covariance and 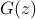 is the input-to-state filter. In other words,
is the input-to-state filter. In other words, 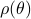 represents the maximal spectral “mass” located at
represents the maximal spectral “mass” located at 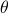 which is consistent with the covariance matrix. It can also be shown that
which is consistent with the covariance matrix. It can also be shown that
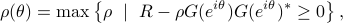
where 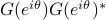 represents the state covariance for the sinusoidal input
represents the state covariance for the sinusoidal input 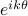 .
The optimal solution is
.
The optimal solution is
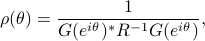
and implemented in envlp.m.
This generalizes the Capon spectral estimation method which applies to 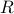 being Toeplitz matrix and
being Toeplitz matrix and 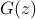 the tapped delay line transfer function. The Capon method may be motivated by a noise suppression formulation aimed at antenna array applications [P. Stoica, R.L. Moses, 1997].
the tapped delay line transfer function. The Capon method may be motivated by a noise suppression formulation aimed at antenna array applications [P. Stoica, R.L. Moses, 1997].
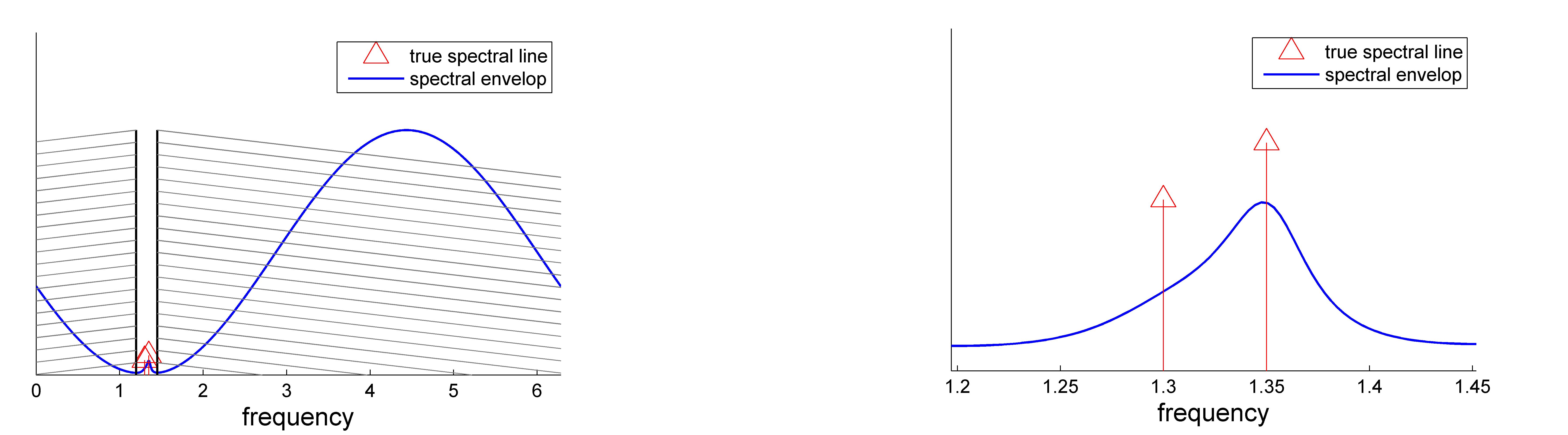
For real valued processes with a symmetric spectrum with respect to the origin, a symmetrized version of the spectral envelop [1] can be similarly obtained:
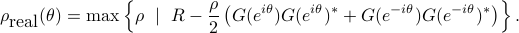
 |