% SIGNAL = sinusoids + noise % Setting up the signal parameters and time history N=100; a0=1.8; a1=1.5; theta1=1.3; a2=2; theta2=1.35; k=1:N; k=k(:); y=a0*randn(N,1)+a1*exp(1i*(theta1*k+2*pi*rand))+a2*exp(1i*(theta2*k+2*pi*rand));
Introduction
Consider a discrete-time zero-mean stationary process  ,
,
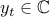 , and
let
, and
let
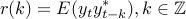
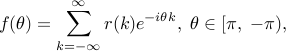
represents power density over frequency. Under suitable smoothness conditions, it is also
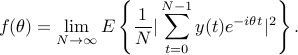
Spectral estimation refers to esimating 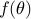 when only
a finite-sized observation record
when only
a finite-sized observation record 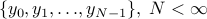 of the time series is available.
Different schools of thoughts have evolved over the years based on varying assumptions and formalisms. Classical methods began first
based on Fourier transform techniques and the periodogram, followed by the so called modern spectral estimation methods
such as the Burg method, MUSIC, ESPRIT, etc.. The mathematics relates to the theory of the Szeg
of the time series is available.
Different schools of thoughts have evolved over the years based on varying assumptions and formalisms. Classical methods began first
based on Fourier transform techniques and the periodogram, followed by the so called modern spectral estimation methods
such as the Burg method, MUSIC, ESPRIT, etc.. The mathematics relates to the theory of the Szeg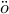 orthogonal polynomials and the stucture od Toeplitz covariances.
orthogonal polynomials and the stucture od Toeplitz covariances.
In contrast, recently, the analysis of state covariance matrices, see e.g. [1, 2], suggested a general framework which alows even higher resolution. A series of generalized spectral estimation tools have been developed generalizing Burg, Capon, MUSIC, ESPRIT, etc.. In the following, we will overview some of these high resolution methods and the relevant computer software. Their use is shown via a representative academic examples.
We want to resolve two sinusoids in based on 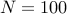 noisy measurements of the time series
noisy measurements of the time series
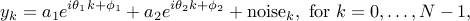
where 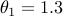 and
and 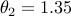 . These are closer than
the theoretical resolution limit
. These are closer than
the theoretical resolution limit 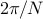 of Fourier method.
of Fourier method.