|
Singular Value Decomposition and
Frequency Responses of PDEs in Chebfun
Introduction
In many physical systems there is a need to examine the effects of
exogenous disturbances on the variables of interest. The frequency
response analysis represents an effective means for quantifying the
system's performance in the presence of a stimulus, and it characterizes
the steady-state response of a stable system to persistent harmonic
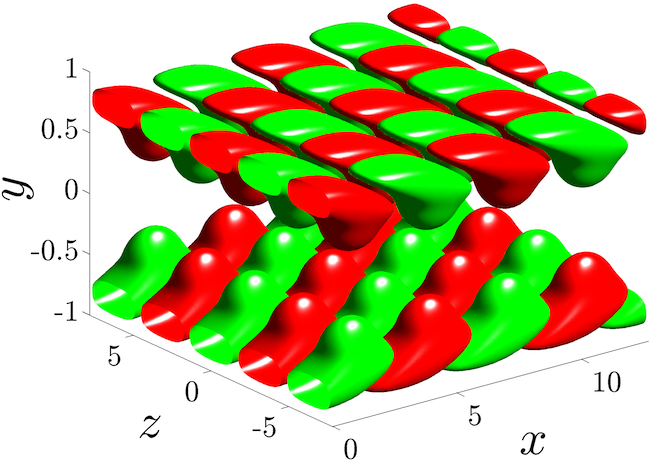
forcing. For infinite dimensional systems, the principal singular value
of the frequency response operator quantifies the largest amplification
from the input forcing to the desired output at each frequency.
Furthermore, the associated left and right principal singular functions
identify the spatial distributions of the output (that exhibits this
largest amplification) and the input (that has the strongest influence
on the system's dynamics), respectively.
We have developed mathematical framework and computational tools for
calculating frequency responses of linear time-invariant partial
differential equations (PDEs) in which an independent spatial variable
belongs to a compact interval. In conventional studies this computation
is done numerically using spatial discretization of differential
operators in the evolution equation. Our method avoids this by recasting
the frequency response operator as a two point boundary value problem
and using state-of-the-art automatic spectral collocation techniques for
solving the resulting eigenvalue problems with accuracy comparable to
machine precision. The algorithm is based on transforming the two point
boundary value problem in differential form into an equivalent integral
representation. Our approach has two advantages over currently available
schemes: first, it avoids numerical instabilities encountered in systems
with differential operators of high order and, second, it alleviates
difficulty in implementing boundary conditions. We refer the users to
[Lieu & Jovanovic, J. Comput. Phys. 2013] for a detailed
explanation of the method.
Even though we confine our attention to computation of the frequency
responses for PDEs, the developed framework allows users to employ
Chebfun as a tool for determining singular value decomposition of
compact operators that admit two point boundary value representations.
In particular, our approach paves the way for overloading Matlab's
command svds, from matrices to compact operators.
We have developed the following easy-to-use Matlab function (an m-file),
svdfr.m
which takes the system's coefficients and boundary condition matrices as
inputs and returns the desired number of left (or right) singular pairs
as the output. The coefficients and boundary conditions of the adjoint
systems are automatically implemented within the code. Thus, the burden
of finding the adjoint operators and corresponding boundary conditions
is removed from the user.
help svdfr
========================================================================
[Sfun,Sval] = svdfr(A0,B0,C0,Wa0,Wb0,LRfuns,Nsigs)
Given a two point boundary value representation of the frequency response
operator
{ A0*phi = B0*d,
T: { u = C0*phi,
{ 0 = Wa0*phi(a) + Wb0*phi(b),
solve the eigenvalue problem
T*Ts*Sfun = Sval*Sfun, or Ts*T*Sfun = Sval*Sfun,
where Ts is the adjoint of the frequency response operator T
{ A0s*psi = B0s*f,
Ts: { g = C0s*psi,
{ 0 = Wa0s*psi(a) + Wb0s*psi(b).
Inputs:
LRfuns = 1 --> solve for left singular functions: T*Ts
--> determine spatial profile of the output
LRfuns = 0 --> solve for right singular functions: Ts*T
--> determine spatial profile of the input
Nsigs --> number of desired singular values (default: Nsigs = 1)
Outputs:
Sval --> singular values of T arranged in descending order
Sfun --> singular functions associated with Sval
Written by: Binh Lieu
Reference:
B. K. Lieu and M. R. Jovanovic
"Computation of frequency responses for linear time-invariant PDEs on a compact interval"
J. Comput. Phys., vol. 250, pp. 246-269, 2013.
========================================================================
|