% State-space representation of the mass-spring system with N = 50 masses N = 50; I = eye(N,N); Z = zeros(N,N); T = toeplitz([2 -1 zeros(1,N-2)]); A = [Z I; -T Z]; B1 = [Z; I]; B2 = [Z; I]; Q = eye(2*N); R = 10*I; % Compute the optimal sparse feedback gains options = struct('method','card','gamval',logspace(-4,0,50),... 'rho',100,'maxiter',100,'blksize',[1 1]); tic solpath = lqrsp(A,B1,B2,Q,R,options); toc
Mass-spring system: cardinality function
 |
Mass-spring system with |
Here, we show the Matlab code and the computational results obtained
using lqrsp.m. In this example, we use the cardinality function 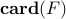 to promote
sparsity. We set
to promote
sparsity. We set 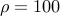 and select
and select 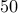 logarithmically-spaced
points for
logarithmically-spaced
points for ![gamma in [10^{-4}, , 1]](eqs/2668613559827723537-130.png) .
.
Matlab code
Computational results
Download Matlab code mass_spring_card.m to reproduce these figures.
Sparsity patterns
The number of nonzero elements in 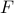 decreases with
decreases with 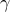 .
.
 |
The number of nonzero elements in the feedback gain |
The number of nonzero sub-diagonals in both position and velocity feedback gains
![F = [F_p ; ; F_v]](eqs/3382737894141789894-130.png) decreases with
decreases with  For large values of
For large values of  both
both 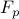 and
and 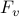 become
diagonal matrices.
become
diagonal matrices.
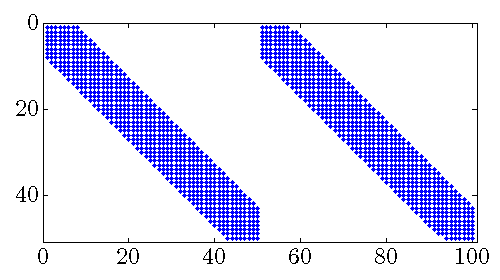 |
Sparsity pattern of the feedback gain matrix
|
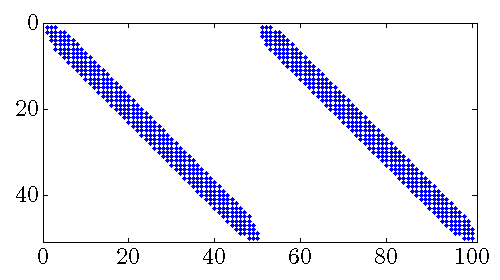 |
Sparsity pattern of the feedback gain matrix |
 |
Sparsity pattern of the feedback gain matrix
|
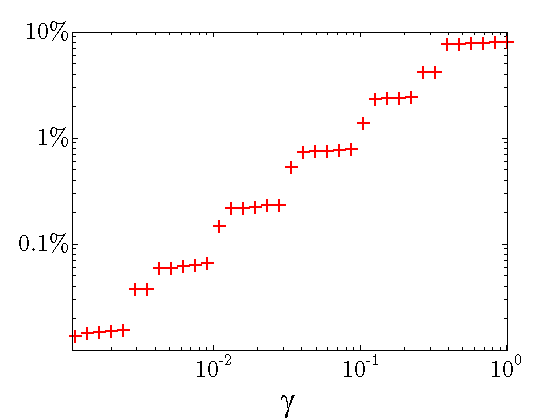
Performance of sparse feedback gains
In the absence of sparsity constraints, i.e., at 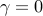 , the optimal
, the optimal 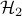 controller
controller
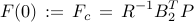
is obtained from the positive definite solution of the algebraic Riccati equation
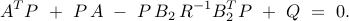
As 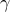 increases, the feedback gain
increases, the feedback gain 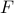 becomes sparser and the
quadratic performance deteriorates.
becomes sparser and the
quadratic performance deteriorates.
 |
Sparsity level:
|
 |
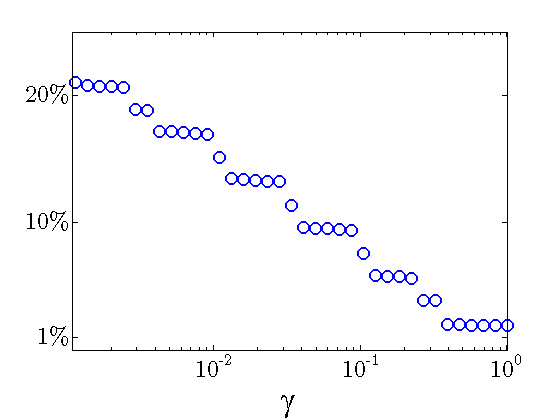
Performance loss:
|
The above results demonstrate that the optimal sparse feedback gain,
with 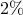 of nonzero elements relative to the centralized feedback gain
of nonzero elements relative to the centralized feedback gain 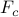 ,
introduces performance loss of only
,
introduces performance loss of only 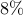 compared to
compared to  .
.
![begin{array}{cccc} gamma & 0.04 & 0.27 & 1.00 [0.35cm] displaystyle{frac{ {rm bf{card}} , (F) }{ {rm bf{card}} , (F_{c}) }} & 9.60 % & 3.92 % & {bf 1.92 %} [0.5cm] displaystyle{ frac{J(F) ,-, J(F_c)}{J(F_c)} } & 0.73 % & 4.14 % & {bf 7.97 % } end{array}](eqs/8579342141338241296-130.png)
Diagonals of sparse feedback gains
The elements on the main diagonals of the optimal sparse feedback gains become larger as the number of
the sub-diagonals of  drops. Thus, in order to compensate for communication with smaller
number of neighboring masses, each mass places more emphasis on its own position and velocity when
forming control action.
drops. Thus, in order to compensate for communication with smaller
number of neighboring masses, each mass places more emphasis on its own position and velocity when
forming control action.
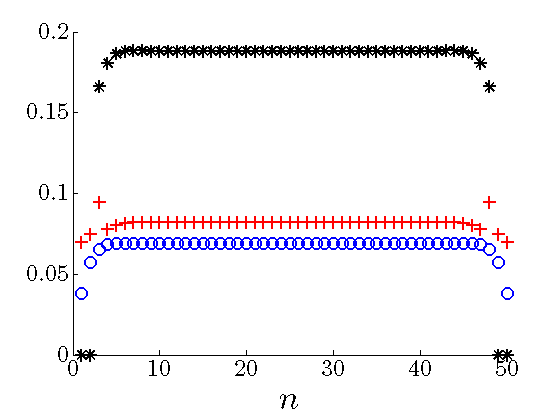 |
Diagonals of the optimal sparse |
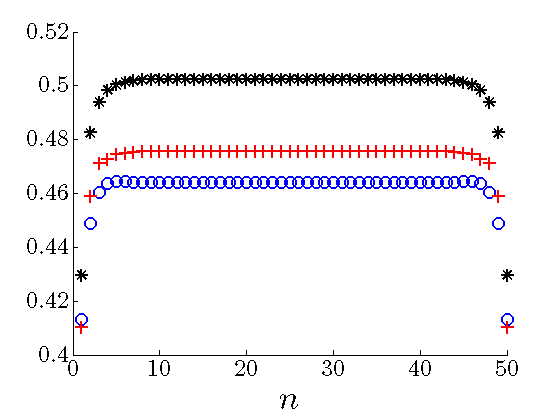 |
Diagonals of the optimal sparse |
Also see computational results obtained using other sparsity-promoting functions.
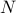 masses on a line.
masses on a line. masses, there are total of
masses, there are total of  elements in
elements in 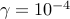 .
.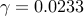 .
.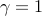 .
.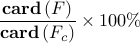
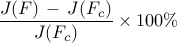
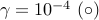 ,
, 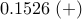 ,
, 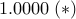 .
.
 norm
norm