Mingyi Hong
 |
Mingyi HongAssociate Professor Email: mhong at umn.edu |
Research Group
Our research group, Optimization for AI Lab (OptimAI-Lab), conduct research on contemporary issues in optimization, information processing and foundation models (Large Language Models, diffusion models, etc).
See here for our publication, and here for the current projects.
Teaching
EE 3015 Signal and Systems, Spring 2019, 2022, UMN, ECE Department
EE 5239 Nonlinear Optimization, Fall 2017, 2018, 2019, 2020, 2021, 2023,2024 UMN, ECE Department
RA and Postdoctoral position available
We have research assistants and post doctoral fellow position available, in the general area of optimization, diffusion models, LLM. If you are interested, please contact Dr. Hong via email
Group News
Sept. 2025, INFORMS Balas Prize: M. Receives the Egon Balas Prize from INFORMS Optimization Society. This prize is awarded annually to an individual for a body of contributions in the area of optimization.
Sept. 2025, new paper on Bilevel optimization: A new paper A Correspondence-Driven Approach for Bilevel Decision-making with Nonconvex Lower-Level Problems, joint work with Xiaotian, Jiaxiang and Shuzhong is available [here]. In this work, we study challenging bilevel optimization problems where the lower-level problem is non-convex.
Sept. 2025, new students joining the group: Welcome Zijian Zhang (ECE) and Shuyu Gan (CSE, co-advised with DK) who joined the group as first-year PhD students.
July 2025, new grant: A new 3-year grant Collaborative Research: Unregistered Spectral Image Fusion in Remote Sensing: Foundations and Algorithms is awarded by NSF (joint work with Xiao); In this work, we develop theory and algorithms for challenging fusion tasks in remote sensing.
July 2025, a talk on bilevel optimization: M. Delivered a semi-plenary talk in ICCOPT 2025. The slides can be find here
June 2025, new paper on parameter efficient pertaining: A new paper A Minimalist Optimizer Design for LLM Pretraining, joint work with Thanos, Jiaxiang and Andi is available [here]. In this work, propose an approach that builds efficient pretraining algorithms from scratch.
May 2025, new grant: A new 2-year grant Invariance in LLM Unlearning Advancing Optimization Foundations for Machine Unlearning is awarded by [Open Philantrophy] (Technical AI Safety Research, joint work with Sijia and Shiyu); In this work, we develop theory and algorithms for LLM unlearning.
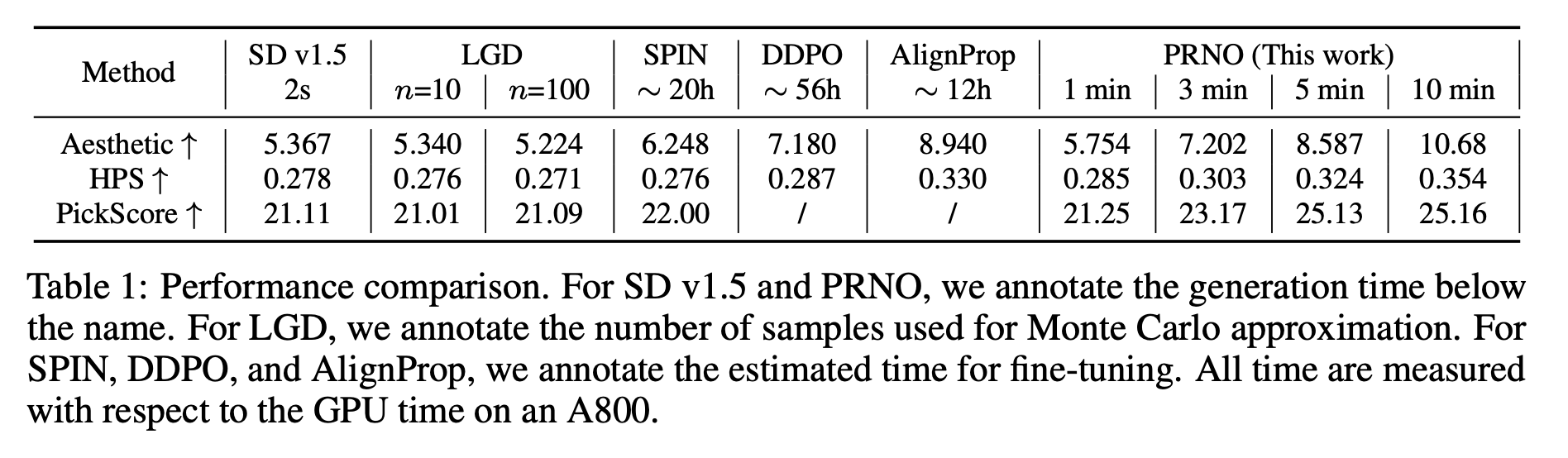
May 2025, new paper on RL for agents: A new paper Reinforcing Multi-Turn Reasoning in LLM Agents via Turn-Level Credit Assignment, joint work with Siliang, Quan, William (Prime Intellect), Oana (Morgan Stanley), Yuriy Nevmyvaka (Morgan Stanley) is available [here]. In this work, we show that it is critical to perform credit assignment when training LLMs for multi-turn agent applications; Please find the code [here]
 |
May 2025, new paper on unlearning: A new paper BLUR: A Bi-Level Optimization Approach for LLM Unlearning, joint work with Hadi, Sijia and Amazon colleagues is available. In this work, we propose a new formulation of the unlearning problem, based on a (simple) bilevel optimization optimization, which can prioritize the unlearning capabilities while maintaining the desirable content from the LLM output. Our extensive experiments demonstrate that BLUR consistently outperforms all the state-of-the-art algorithms across various unlearning tasks, models, and metrics. Please find the code [here]
 |
May 2025, new survey paper on alignment: Our survey paper Aligning Large Language Models with Human Feedback: Mathematical Foundations and Algorithm Design, joint work with Siliang, Luca, Chenliang, Jiaxiang, Volkan (EPFL), Stephano (Stanford), Markus (Google) and Alfredo (TAMU), on algorithmic foundations and perspective from inverse RL for LLM alignment has been uploaded online; Please find the paper here [here]
May 2025, new preprint entitled RoSTE: An Efficient Quantization-Aware Supervised Fine-Tuning Approach for Large Language Models, joint work with Quan, Oscar, Hoi-To, Kati and Yungsuk, is available; see the preprint [here]. In this work, we develop a novel algorithm for performing quantization while doing SFT for LLM finetuning. Our method, named RoSTE, consistently achieves superior performances across various tasks and different LLM architectures as compared with the SOTA algorithms. See code [here].
 |
April 2025: 5 papers accepted by ICML 2025. Congratulations to everyone!
“RoSTE: An Efficient Quantization-Aware Supervised Fine-Tuning Approach for Large Language Models” see the paper [here], joint work with Quan, Oscar, To, Katie and Yungsuk
“Inference-Time Alignment of Diffusion Models with Direct Noise Optimization” see the paper [here], joint work with Zhiwei and Jon and Tsung-Hui
“Towards LLM Unlearning Resilient to Relearning Attacks: A Sharpness-Aware Minimization Perspective and Beyond” see the paper [here] , join work with Chongyu, Sijia, Anil, Yihua.
“On the Vulnerability of Applying Retrieval-Augmented Generation within Knowledge-Intensive Application Domains” see the paper [here], joint work with Jie, Xun, Ganghua, Xuan and researchers from Cisco.
“BRiTE: Bootstrapping Reinforced Thinking Process to Enhance Language Model Reasoning”, see the paper [here], joint work with Han et al with Zhaoran's group
April 2025 new preprint (with Prashant, Ioannis, Yihua and Sijia) entitled A Doubly Stochastically Perturbed Algorithm for Linearly Constrained Bilevel Optimization is available; see the preprint [here]. In this work, we develop a novel perturbation strategy that solves a linearly constrained bilevel problem, and analyzed their convergence guarantees.
 |
Feb. 2025:, 3 papers accepted by ICLR 2025. Congratulations to everyone!
“DiSK: Differentially Private Optimizer with Simplified Kalman Filter for Noise Reduction” see the paper [here], joint work with Xinwei, Meisam, and Researchers from Google and Amazon
“Do LLMs Recognize Your Preferences? Evaluating Personalized Preference Following in LLMs” see the paper [here] , join work with Siyan, Kaixiang, and researchers from Amazon. (Oral paper)
“Joint Reward and Policy Learning with Demonstrations and Human Feedback Improves Alignment” see the paper [here], joint work with Siliang, Chenliang, Alfredo, Dongyeop and Zeyi. (Spotlight paper)
Jan. 2025 new preprint (with Xiaotian, Jiaxiang and Shuzhong) entitled Barrier Function for Bilevel Optimization with Coupled Lower-Level Constraints: Formulation, Approximation and Algorithms is available; see the preprint [here]; We introduce a novel approach for bilevel optimization tackling: (1) Strongly convex lower-level problems; (2) Linear programming lower levels (e.g., price setting – first to address this!) We require only the most basic assumptions. Our barrier function method guarantees non-asymptomatic convergence. Validated by experiments.
The following is the problem we consider, and the reformulated problem we consider:
 |
 |
Jan. 2025 : Congratulation to Songtao, who joins the Chinese University of Hong Kong Computer Science Department as an Assistant Professor.
Jan. 2025, IEEE Fellow: M. is elected to IEEE Fellow with the citation “for contributions to optimization in signal processing, wireless communication and machine learning”.
Jan. 2025, student fellowship: Congratulations to Quan and Xinnan for receiving the Amazon Machine Learning System Fellowship ! This fellowship awards students who will contribute to research advancing the science of computer systems and/or software systems support for machine learning and artificial intelligence.
Dec. 2024, new grant: A new 2-year grant ACED: Building Molecule Generative Models for Drug Development via Conditional Diffusion and Multi-Property Optimization is awarded by NSF; In this work, we develop optimization-based computational methods to align diffusion model generation with desired drug properties, so to enable efficient molecule generation and drug discovery.
Nov. 2024, new grant: A new 3-year grant Inverse Reinforcement Learning with Heterogeneous Data: Estimation Algorithms with Finite Time and Sample Guarantees is awarded by NSF; In this work, we develop theory and algorithms for LLM alignment (e.g., RLHF, DPO, etc) from inverse reinforcement learning perspective.
Nov. 2024:, Congratulations to Siliang and Songtao to receive the prestigious IBM Pat Goldberg Memorial Award (honorable mention), for our 2022 NeurIPS paper A Stochastic Linearized Augmented Lagrangian Method for Decentralized Bilevel Optimization [here]; see the IBM announcement [here].
Oct. 2024, Cisco Research Award: We are honored to be awarded a Cisco research award to investigate inference-time LLM alignment problems.
Oct. 2024 new preprint (with Xinwei, Meisam and Google Research collaborators) entitled Disk: Differentially private optimizer with simplified Kalman filter for noise reduction is available; see the preprint [here]; This work propose a novel idea of leveraging Kalman Filter to reduce the noise for the DP algorithms; it achieves new state-of-the-art results across diverse tasks, including vision tasks such as CIFAR100 and ImageNet-1k and language fine-tuning tasks such as GLUE, E2E, and DART.
 |
Oct. 2024 paper accepted (OR):, our work Structural Estimation of Markov Decision Processes in High-Dimensional State Space with Finite-Time Guarantees (joint work with Alfredo and Siliang) has been accepted by Operations Research. See the paper link [here] This work discussed a set of new algorithms, based on bilevel optimization theory, for the problem of inverse RL.
Oct. 2024 new preprint (with Amazon AGI collaborators) entitled Unlearning as multi-task optimization: A normalized gradient difference approach with an adaptive learning rate is available; see the preprint [here]; This work develops a novel multi-task perspective to LLM unlearning problem, and is able to establish state-of-the-art unlearning performance for both TOFU and MUSE datasets.
 |
Sept 2024, Group Kayak Activity, with visiting student Chung You Yau from CUHK.
 |
Sept. 2024:, 7 papers accepted by NeurIPS 2024. Congratulations to everyone!
“Defensive Unlearning with Adversarial Training for Robust Concept Erasure in Diffusion Models” see the paper [here]
“Pre-training Differentially Private Models with Limited Public Data” see the paper [here]
“DOPPLER: Differentially Private Optimizers with Low-pass Filter for Privacy Noise Reduction” see the paper [here]
“Getting More Juice Out of the SFT Data: Reward Learning from Human Demonstration Improves SFT for LLM Alignment” see the paper [here]
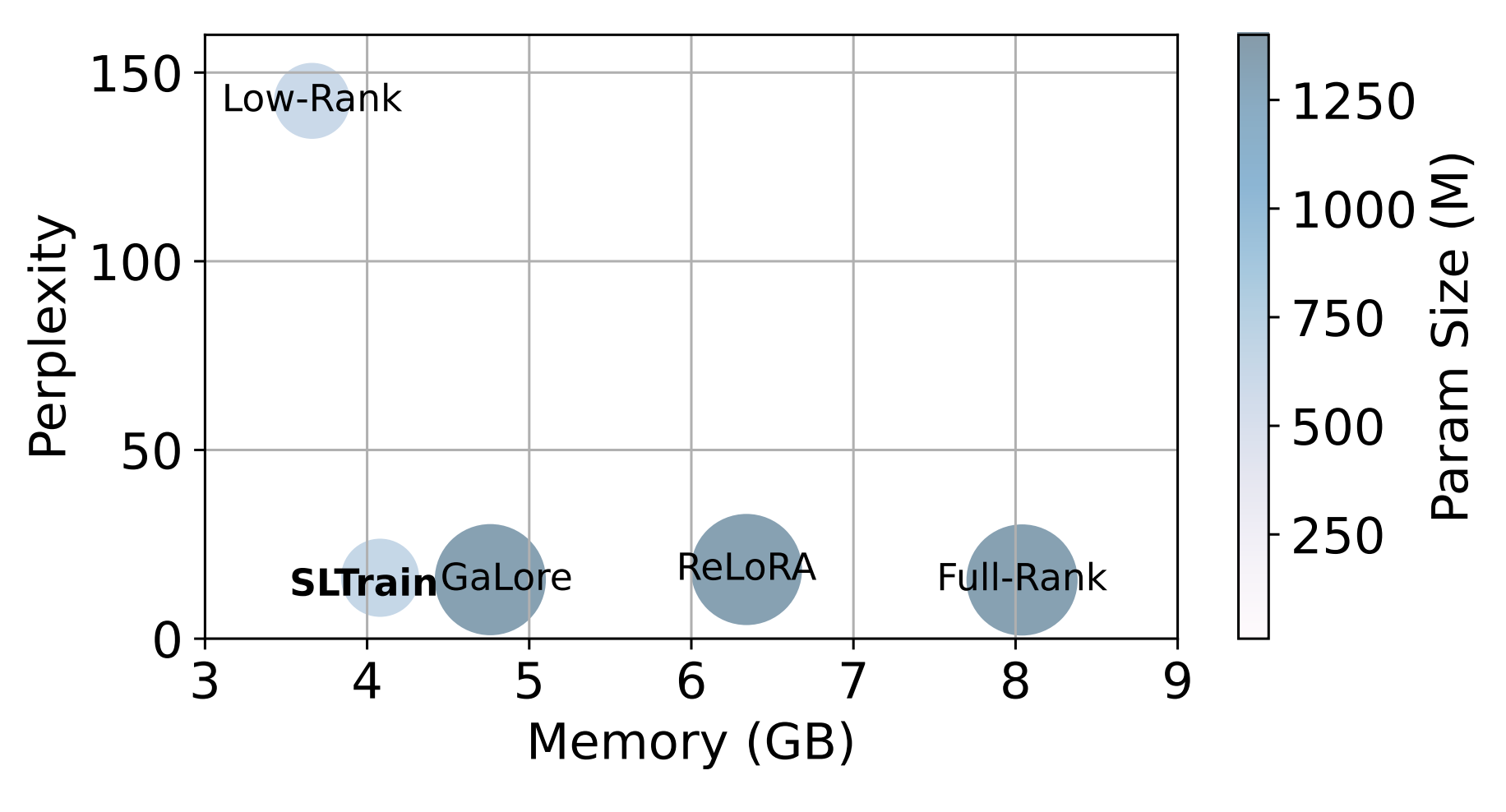
“SLTrain: a sparse plus low rank approach for parameter and memory efficient pretraining” see the paper [here]
“Unraveling the Gradient Descent Dynamics of Transformers” see the paper [here]
“RAW: A Robust and Agile Plug-and-Play Watermark Framework for AI-Generated Images with Provable Guarantees” see the paper [here]
August. 2024:, Congratulations to Jiaxiang to receive the prestigious IFORMS Computing Society Best Paper Award!
July. 2024, new grant: A new 3-year grant Bi-Level Optimization for Hierarchical Machine Learning Problems: Models, Algorithms and Applications is awarded by NSF; In this work, we develop theory and algorithms for bilevel optimization, and identify applications of bilevel problems to machine learning and language models.
June. 2024, survey paper accepted (JSAC): our work A survey of recent advances in optimization methods for wireless communications (joint work with Ya-Feng, Tsung-Hui, Anthony, Wei, Eduard, Zheyu) has been accepted by IEEE JSAC, together with the special issue we organized about optimization for wireless systems; see the paper [here]
June. 2024 new preprint (with Andi, Jiaxiang, Wei, Akiko, Pratik and Bamdev) entitled SLTrain: a sparse plus low-rank approach for parameter and memory efficient pretraining has been submitted for publication; see the preprint [here]; This work shows that, by using sparse+low rank techniques, retraining can be made very memory efficient.
 |
June. 2024 new preprint (with Zhiwei, Jon, Tsung-Hui) entitled Tuning-Free Alignment of Diffusion Models with Direct Noise Optimization has been submitted for publication; see the preprint [here]; This work develop a novel direct noise optimization method that can efficiently assign the output of diffusion models.
 |
 |
June. 2024 new preprint (with Jiaxiang, Siliang, Hoi-To, Chenliang, and Alfredo) entitled Getting More Juice Out of the SFT Data: Reward Learning from Human Demonstration Improves SFT for LLM Alignment has been submitted for publication; see the preprint [here]; This work shows that, by building a reward model for SFT stage, one can significantly improve the SFT performance.
 |
May 2024, NSF sponsored workshop, Midwest Machine Learning Symposium held at Minneapolis, organized by M. and Ju Sun ant others; See [Symposium Website]; The symposium is free for all participants and provide lodgings; It attracted 300+ participants from all over midwest region.
May. 2024:, three papers accepted by ICML 2024
MC: Efficient MCMC Negative Sampling for Contrastive Learning with Global Convergence, with CY Yau, HT Wai, P Raman and S Sarkar, see the paper here [here]
Revisiting Zeroth-Order Optimization for Memory-Efficient LLM Fine-Tuning: A Benchmark, with Yihua Zhang, Pingzhi Li, Junyuan Hong, Jiaxiang Li, Yimeng Zhang, Wenqing Zheng, Pin-Yu Chen, Jason D Lee, Wotao Yin, Zhangyang Wang, Sijia Liu, Tianlong Chen; see the paper here [here]
MADA: Meta-Adaptive Optimizers through hyper-gradient Descent with K Ozkara, C Karakus, P Raman, M Hong, S Sabach, B Kveton, V Cevher, see the paper here [here]
April. 2024:, congratulations to Siliang Zeng to be awarded the prestigious Doctoral Dissertation Fellowship
April. 2024 M. And Sijia and Ping-Yu delivered proposal “Zeroth-Order Machine Learning: Fundamental Principles and Emerging Applications in Foundation Models” at ICASSP 2024.
April. 2024 M. Gave a talk “Old and New Optimization Techniques for Foundation Model Fine-Tuning and (continual) Pre-Training” at ECE@Ohio State; details are [here].
Jan. 2024, AWS Research Award: We have been honored to be awarded an AWS research award to investigate LLM optimization related topics.
Jan. 2024, Cisco Research Award: We have been honored to be awarded a Cisco research award to investigate robustness and trustworthy issues for diffusion models.
Dec 2023, Group at NeurIPS 2023, presented an oral paper on inverse reinforcement learning (0.4% of overall submitted papers)
 |
Dec. 2023 new preprint (with Xinwei, Steven and Woody) entitled Differentially Private SGD Without Clipping Bias: An Error-Feedback Approach has been submitted for publication; see the preprint here; This work shows that, by using error feedback, the bias of clipping gradient can be completely removed, while being able to use arbitrary clipping threshold (independent of the problem). These properties makes it practical to use the algorithm in practice (as compared with DP-SGD).
Dec 2023, Dr. Jiaxiang Li from Math Department of UC Davis has joined our group as a Post-Doctoral Fellow. Welcome Jiaxiang!
Dec 2023, NSF sponsored workshop on sensing and analytics will be help Dec 7-8 in DC NSF headquarters; See [Workshop Website]
Nov 2023, Xinwei has successfully defended his PhD thesis; Xinwei has made some exciting achievements during his PhD career, and he will be joining USC for a postdoctoral fellowship; see his [publications]; Congrats Dr. Zhang!
 |
Nov. 2023, paper accepted (TAC): our work On the local linear rate of consensus on the stiefel manifold (joint work with Sixiang, Alfredo and Shahin) has been accepted by IEEE TAC; see the paper [here]
Oct. 2023, tutorial proposal accepted. Our tutorial proposal “Zeroth-Order Machine Learning: Fundamental Principles and Emerging Applications in Foundation Models” has been accepted by ICASSP 2024 and AAAI 2024.
Sept 2023, Group Kayak Activity, with visiting student Zhiwei Tang
 |
Sept. 2022, paper accepted: Four papers have been accepted by NeurIPS 2023.
Understanding Expertise through Demonstrations: A Maximum Likelihood Framework for Offline Inverse Reinforcement Learning (joint work with Siliang, Chenliang and Alfredo) has been accepted as an Oral paper; see the paper here [here]
Vcc: Scaling Transformers to 128K Tokens or More by Prioritizing Important Tokens (joint work with Zhanpeng and AWS researchers); see the paper here [here]
Selectivity Drives Productivity: Efficient Dataset Pruning for Enhanced Transfer Learning (joint work with Yihua et al)
A Unified Framework for Inference-Stage Backdoor Defense (joint work with Sun, Ganghua, Xuan, Jie and Cisco researchers).
July. 2023, new grant: We got a grant to organize an NSF workshop on “the Convergence of Smart Sensing Systems, Applications, Analytic and Decision Making”; the workshop website will be online soon.
July. 2023, new grant: We obtained a new 3-year grant “A Multi-Rate Feedback Control Framework for Modeling, Analyzing, and Designing Distributed Optimization Algorithms” from NSF; In this work, we advocate the a generic “model” of distributed algorithms (based on techniques from stochastic multi-rate feedback control), which can abstract their important features (e.g., privacy preserving mechanism, compressed communication, occasional communication) into tractable modules.
June 2023, We have bee presented the SPS Best Paper Award and the Pierre-Simon Laplace Early Career Technical Achievement Award at ICASSP 2023. Congratulations to everyone, especially former members from our group, Dr. Haoran Sun and Dr. Xiangyi Chen!
 |
 |
May. 2023, new grant:, M. Is the co-PI for the UMN-lead AI-Climate Institute; this is a 5-year project funded by NSF, NIFA and USDA focusing on climate-smart agriculture and forestry.
April. 2023, paper accepted (TSP): our work Towards Understanding Asynchronous Advantage Actor-critic: Convergence and Linear Speedup (joint work with Tianyi, Hen and Kaiqing) has been accepted by IEEE TSP; see the paper [here]
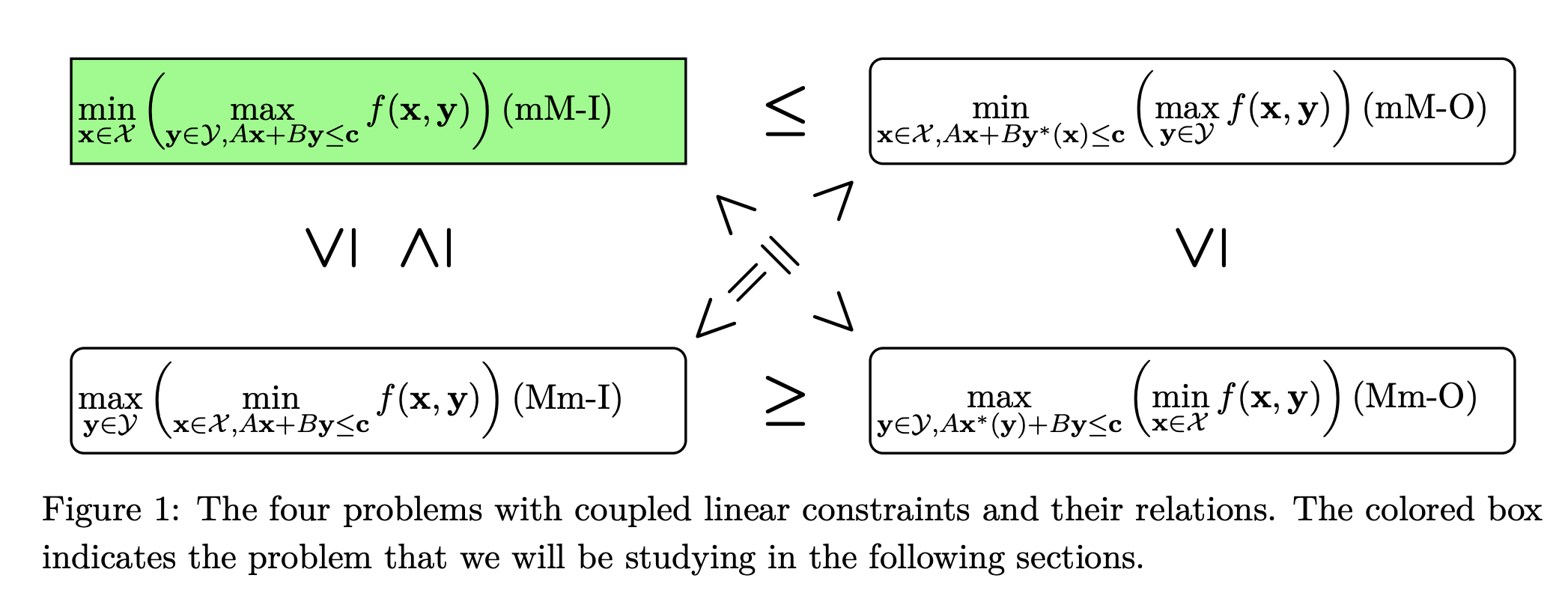
April. 2023, paper accepted (SIOPT): our work Minimax problems with coupled linear constraints: computational complexity, duality and solution methods (joint work with Ioannis and Shuzhong) has been accepted by SIAM Journal on Optimization. In this work, we analyzed a class of seemingly easy min-max problems, where there is a linear constraint coupling the min and max optimization variables. We show that this class of problem is NP-hard, and then derived a duality theory for it. Leveraging the resulting duality-based relaxations, we propose a family of efficient algorithms, and test them on the network interdiction problems. see the paper [here]
 |
April 2023, papers accepted (ICML 2023):
Linearly Constrained Bilevel Optimization: A Smoothed Implicit Gradient Approach with Ioannis and Prashant, Sijia, Yihua and Kevin
FedAvg Converges to Zero Training Loss Linearly for Overparameterized Multi-Layer Neural Networks, with Bingqing, Xinwei, and Prashant
Understanding Backdoor Attacks through the Adaptability Hypothesis, with Xun, Jie, and Xuan and Cisco team
Jan. 2023 new preprint (with Siliang, Chenliang and Alfredo) entitled Understanding Expertise through Demonstrations: A Maximum Likelihood Framework for Offline Inverse Reinforcement Learning has been submitted for publication; see the preprint here; This work develops one of the first offline inverse reinforcement learning (IRL) formulation and algorithm for inferring an agent's reward function, while finding its policy.
 |
Dec. 2022, SPS Early-Career Award: M. Receives the Pierre-Simon Laplace Early Career Technical Achievement Award from IEEE Signal Processing Society.
Dec. 2022, SPS Best Paper Award: our work Learning to optimize: Training deep neural networks for interference management (joint work with Haoran, Xiangyi, Qingjiang, Nikos and Xiao), published in IEEE TSP 2018, has been awarded the 2022 Signal Processing Society Best Paper Award.
Dec. 2022, papers accepted (TSP & TWC): our work Parallel Assisted Learning (joint work with Xinran, Jiawei, Yuhong and Jie Ding) has been accepted by TSP; see the paper [here]; Also, our work Learning to beamform in heterogeneous massive MIMO networks (joint work with Minghe and Tsung-Hui) has been accepted by TWC; see the paper [here]
Nov. 2022, paper conditionally accepted (SIOPT): our work Primal-Dual First-Order Methods for Affinely Constrained Multi-Block Saddle Point Problems (joint work with Junyu, Mengdi and Shuzhong) has been conditionally accepted by SIAM Journal on Optimization (with minor revision)
Nov. 2022, paper conditionally accepted (SIOPT): our work Minimax problems with coupled linear constraints: computational complexity, duality and solution methods (joint work with Ioannis and Shuzhong) has been conditionally accepted by SIAM Journal on Optimization (with minor revision); see the paper [here]
Nov. 2022, paper accepted (SIOPT): our work Understanding a class of decentralized and federated optimization algorithms: A multi-rate feedback control perspective (joint work with Xinwei and Nicola) has been accepted by SIAM Journal on Optimization; see the paper [here]
Oct. 2022, tutorial proposal accepted: with Sijia, Yihua and Bingqing, we will be presenting a tutorial on bilevel optimization in machine learning for AAAI 2023.
Sept. 2022, research award: Our group (together with Jie, Zhi-Li and Prashant) has received a new Meta Research Award, to support our work on developing large-scale distributed algorithms and systems for autoscaling.
Aug. 2022, paper accepted: Five papers have been accepted by NeurIPS 2022.
Advancing Model Pruning via Bi-level Optimization with Yihua, Sijia, Yanzhi, Yugang, et al
Maximum-Likelihood Inverse Reinforcement Learning with Finite-Time Guarantees, with Siliang, Chenliang, and Alfredo
Distributed Optimization for Overparameterized Problems: Achieving Optimal Dimension Independent Communication Complexity, with Bingqing, Ioannis, Hoi-To, and Chung-Yiu
Inducing Equilibria via Incentives: Simultaneous Design-and-Play Ensures Global Convergence, with Boyi, Jiayang, Zhaoran, Zhuoran, Hoi-To, et al
A Stochastic Linearized Augmented Lagrangian Method for Decentralized Bilevel Optimization, with Songtao, Siliang, et al
Aug. 2022, paper accepted (TSP): our work FedBCD: A Communication-Efficient Collaborative Learning Framework for Distributed Features (joint work with researchers at WeBank) has been accepted by TSP; see the paper [here]
Aug. 2022, paper accepted (SIOPT): our work A two-timescale framework for bilevel optimization: Complexity analysis and application to actor-critic (joint work with Hoi-To, Zhaoran and Zhuoran) has been accepted by SIAM Journal on Optimization; see the paper [here]
Aug. 2022, paper award (UAI): our work Distributed Adversarial Training to Robustify Deep Neural Networks at Scale (joint work with IBM researchers), published in The Conference on Uncertainty in Artificial Intelligence (UAI) 2022, has been selected as oral presentation, and selected as the Best Paper Runner-Up Award for the conference; the paper can be found [here]
June 2022, paper accepted (SIOPT): our work On the divergence of decentralized non-convex optimization (joint work with Siliang, Junyu and Haoran) has been accepted by SIAM Journal on Optimization; see the paper [here]
May 2022, We have been virtually presented the SPS Best Paper Award at ICASSP 2022.
May 2022, Prashant will be starting his position at CS Department of Wayne State University; congrats Dr. Khanduri!
May 2022, Xiangyi has successfully defended his PhD thesis; Xiangyi has made some exciting achievements during his PhD career; see his [publications] congrats Dr. Chen!
April 2022, paper accepted: Three papers have been accepted by ICML 2022
A Stochastic Multi-Rate Control Framework For Modeling Distributed Optimization Algorithms with Xinwei, Sairaj and Nicola
Understanding Clipping for Federated Learning: Convergence and Client-Level Differential Privacy, with Xiangyi, Xinwei, and Steven
Revisiting and advancing fast adversarial training through the lens of bi-level optimization, with Yihua, Sijia, Prashant and Siyu
April 2022, Xinwei has received the University of Minnesota's Doctoral Dissertation Fellowship; congrats Xinwei!
Feb. 2022, paper published (TSP): Our work (with Wenqiang, Shahana and Xiao) entitled Stochastic mirror descent for low-rank tensor decomposition under non-Euclidean losses has been published in TSP.
Dec. 2021, SPS Best Paper Award: our work Multi-agent distributed optimization via inexact consensus ADMM (joint work with Tsung-Hui and Xiangfeng), published in IEEE TSP 2016, has been awarded the 2021 Signal Processing Society Best Paper Award.