Mechanism Design for Complex Systems: A Black-box Model Approach
AFOSR, Grant No. 15RT0767, 2015-2019
Goal: Investigate fundamental research questions of mechanism design with a “black-box model”
Abstract: Many complex resource allocation problems require vast amounts of distributed input information, which is proprietary to stakeholders. A resource allocation of this kind – with incomplete information about stakeholders" private information – is an optimization problem with a game-theoretic twist: a stakeholder may misrepresent their input information if this course of action is to her/his own gain. This kind of behavior results in a highly suboptimal allocation of resources. Designing rules of interaction between the resource allocator and the stakeholders (players) so that an optimal allocation can be implemented (without the possibility of input manipulation) is the overarching goal of mechanism design.
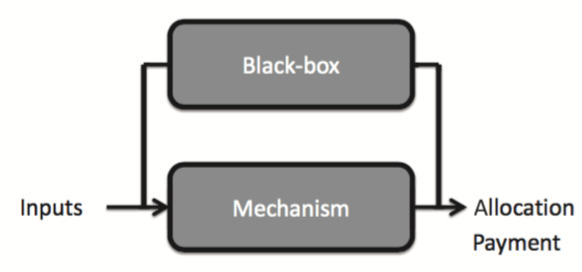 |
An optimal mechanism design is a game whose rules are designed by the resource allocator so that in equilibrium the desired outcome (i.e. optimal allocation) is obtained. A mechanism is said to be incentive compatible (IC) if it is in each player“s best interest to report input private information truthfully. In large-scale complex engineering systems, an additional layer of complexity pertains to the case in which there is no closed-form analytical expression for evaluating different resource allocation strategies. In many complex resource allocation problems this evaluation can only be achieved by repeatedly running a simulation model. This is akin to sequentially querying an ”oracle“ or ”black-box". Hence, in this context a mechanism design must interact with a black-box model as represented Figure. |
To illustrate a concrete application of the problem of mechanism design with black-box interaction, consider the allocation of National Airspace System“s (NAS) capacity pursuant to disruption such as severe weather incident that reduces available capacity. The short-term imbalance in route demands versus capacity must be solved within a short time-span. To maximize allocation efficiency, the NAS manager may direct some airlines” flights with lower costs associated to delays to incur a ground-delay and thus allocate limited routing capacity to other airlines“ flights with higher delay associated costs. This type of resource management strategy relies on (i) complete information on the different airlines” preferences regarding delay and (ii) the ability to evaluate non-linear tradeoffs in the allocation of available routing capacity. In practice, the network resource manager does not have complete information on the different airlines" delay associated costs. Nor does it have access to a closed-form analytical expression for evaluating capacity tradeoffs.
This motivates us to investigate fundamental research questions of mechanism design with a “black-box model” for evaluating different allocation strategies. In the proposed research we consider a design that takes the form of an iterative auction. In such auction the players (stakeholders) are asked to report desired levels of capacity at each round and the auctioneer checks the feasibility of the resulting allocation by consulting a “black-box” and updates prices accordingly.
Related Pulication
Mingyi Hong, “Decomposing Nonconvex Problems Using a Proximal Primal-Dual Approach: Algorithms, Convergence, and Applications”, working paper, available at [arXiv.org], April 2016
Mingyi Hong and Tsung-Hui Chang, “Stochastic Proximal Gradient Consensus Over Random Networks” available at [arXiv.org], Nov, 2015
Alfredo Garcia and Mingyi Hong, “Efficient Rate Allocation in Wireless Networks Under Incomplete Information”, IEEE Transactions on Automatic Control, Vol. 61, No. 5, pages 1397 - 1402, 2016.