Topology identification and optimal design of noisy consensus networks

Sepideh Hassan-Moghaddam and Mihailo R. Jovanovic

Abstract

We study an optimal control problem aimed at achieving a desired tradeoff between the network coherence and communication requirements in the distributed controller. Our objective is to add a certain number of edges to an undirected network, with a known graph Laplacian, in order to optimally enhance closed-loop performance. To promote controller sparsity, we introduce 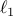-regularization into the optimal 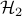formulation and cast the design problem as a semidefinite program. We derive a Lagrange dual and exploit structure of the optimality conditions for undirected networks to develop three customized algorithms that are well-suited for large problems. These are based on the infeasible primal-dual interior-point, the proximal gradient, and the proximal Newton methods. We illustrate that all of our algorithms significantly outperform the general-purpose solvers and that the proximal methods can solve the problems with more than million edges in the controller graph in a few minutes, on a PC. 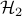We also exploit structure of connected resistive networks to demonstrate how additional edges can be systematically added in order to minimize the norm of the closed-loop system.

Reference

1. Topology identification and optimal design of noisy consensus networks
   S. Hassan-Moghaddam and M. R. Jovanovic
   IEEE Trans. Control Netw. Syst., 2016; submitted, also arXiv:1506.03437v2