Screeching supersonic jet
 |
Temperature contours on a centerplane cross section taken from a
snapshot of the screeching jet. Time histories of pressure were
recorded at probe locations indicated by circles |
Screech is a component of supersonic jet noise that is connected to the presence of a train of shock cells within the jet column. For a turbulent jet, the unsteady shear layers interact with the shocks to create sound. While this process is generally broadbanded, screech is a special case of shock-noise that arises from the creation of a feedback loop between the upstream-propagating part of the acoustic field and the generation of new disturbances at the nozzle lip. This self-sustaining feedback loop leads to an extremely loud (narrow-banded) screech tone at a specific fundamental frequency. The presence of a tonal process embedded in an otherwise broadbanded turbulent flow makes the screeching jet an excellent test case for the sparsity-promoting DMD method. The objective of the developed method is to extract the entire coherent screech feedback loop from the turbulent data and to describe the screech mechanism with as few modes as possible.
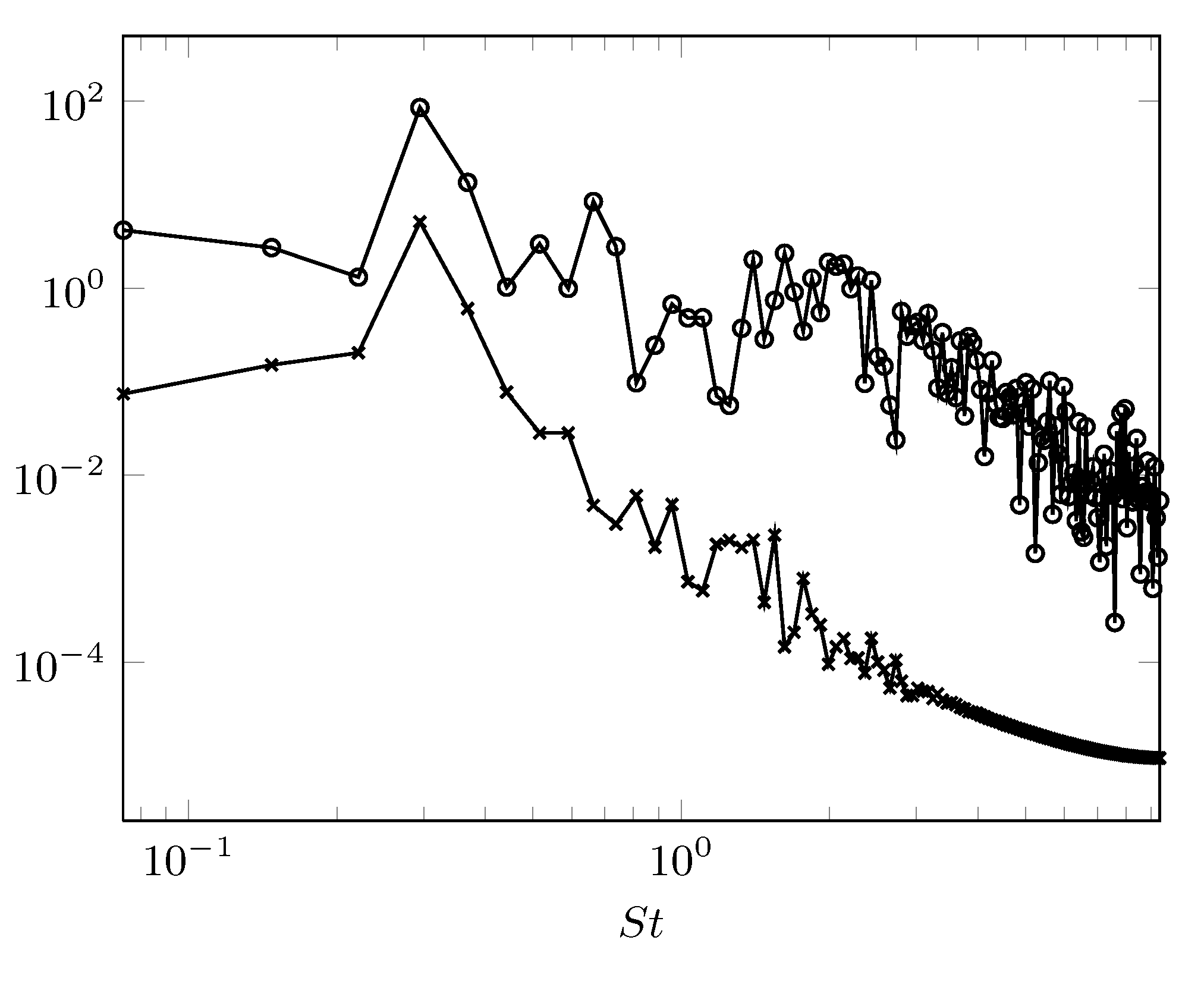 |
Power spectra of pressure corresponding to the measurement locations
indicated in top figure. While both spectra peak at Strouhal number |
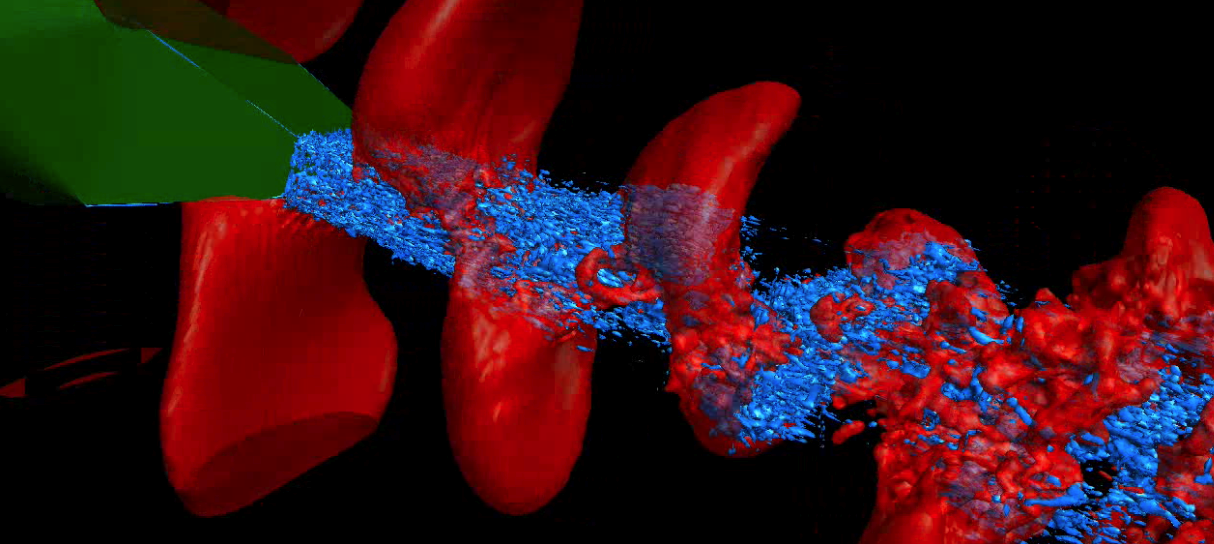 |
The three-dimensional DMD mode associated with the dominant frequency
(that corresponds to the fundamental frequency of the screech tone, |
 |
Dependence of the absolute value of the DMD amplitudes |
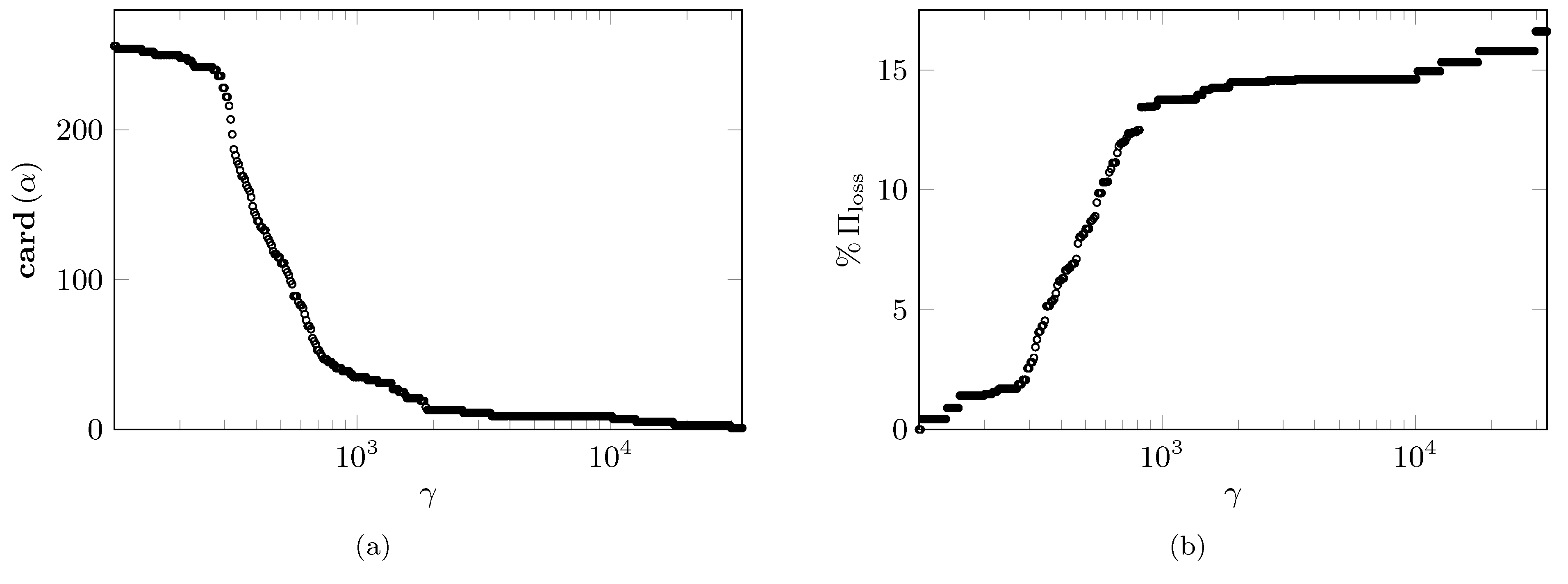 |
(a) The sparsity level |
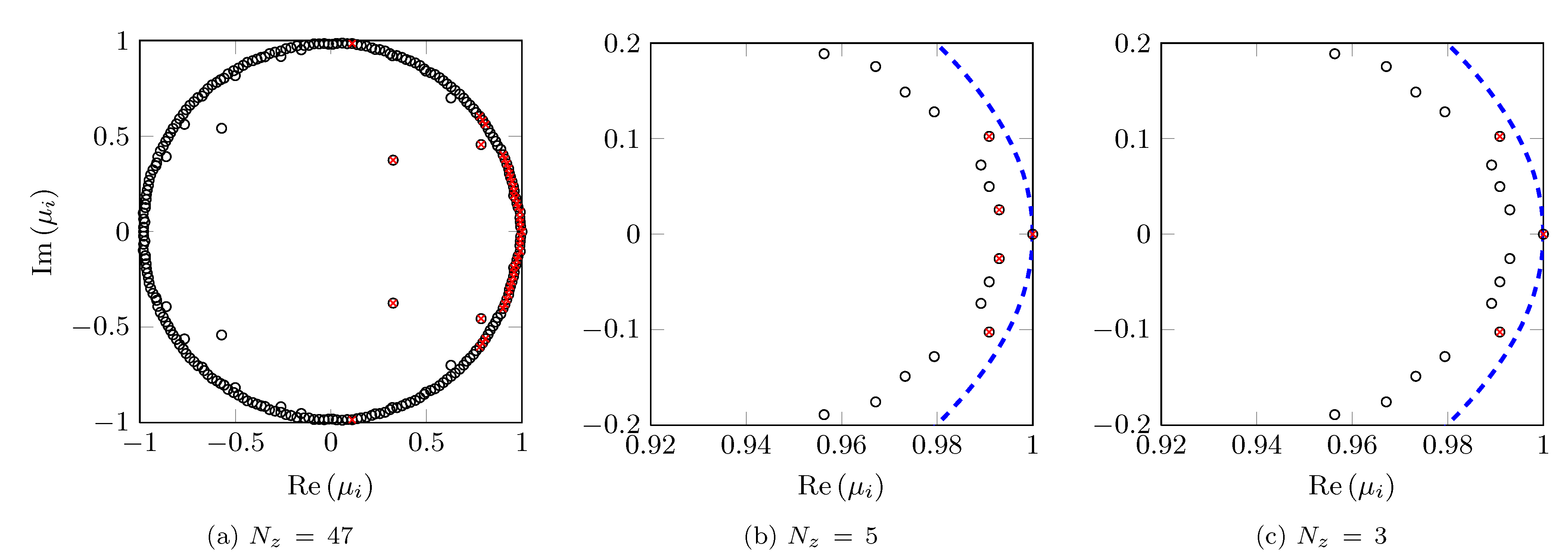 |
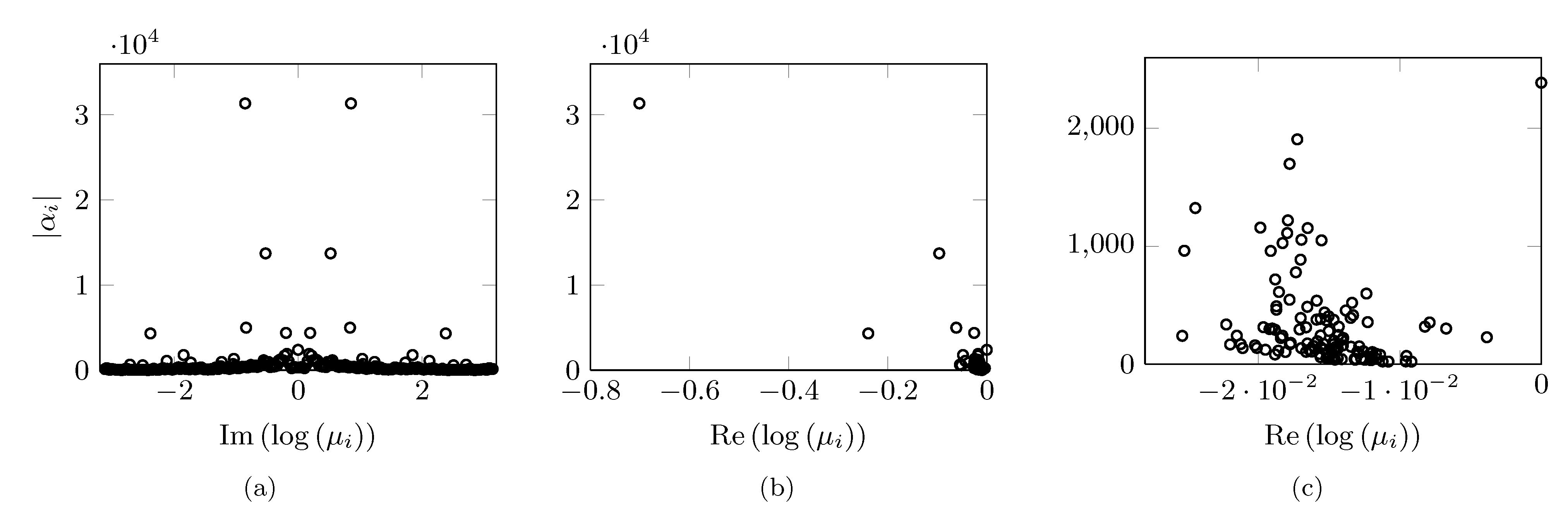
Eigenvalues resulting from the standard DMD algorithm (circles) along
with the subset of |
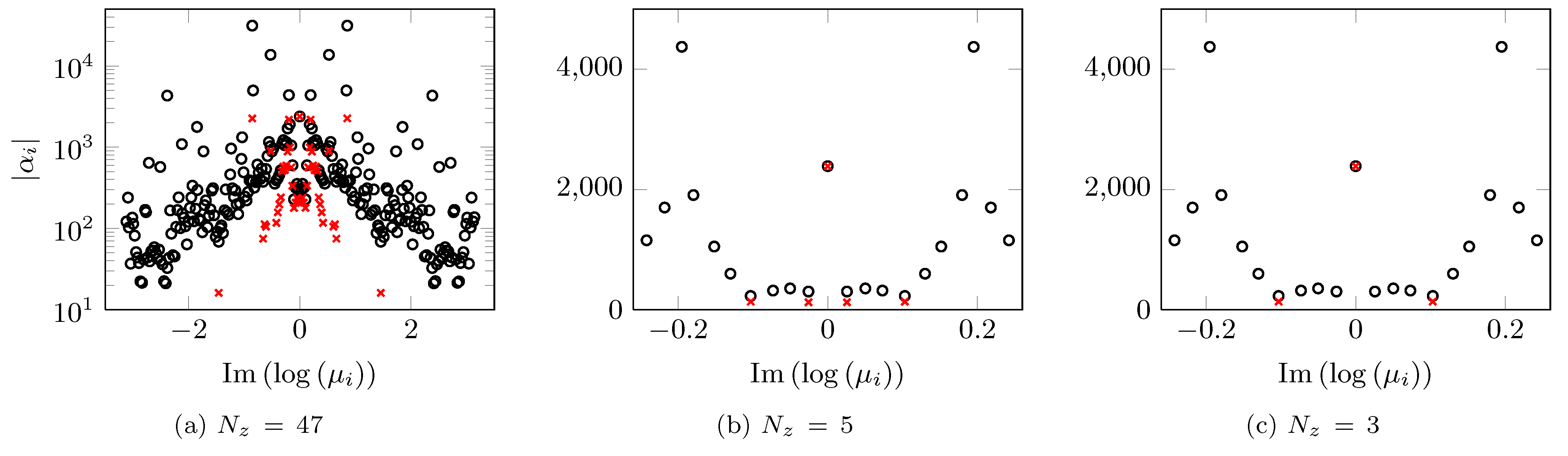 |
Dependence of the absolute value of the amplitudes |
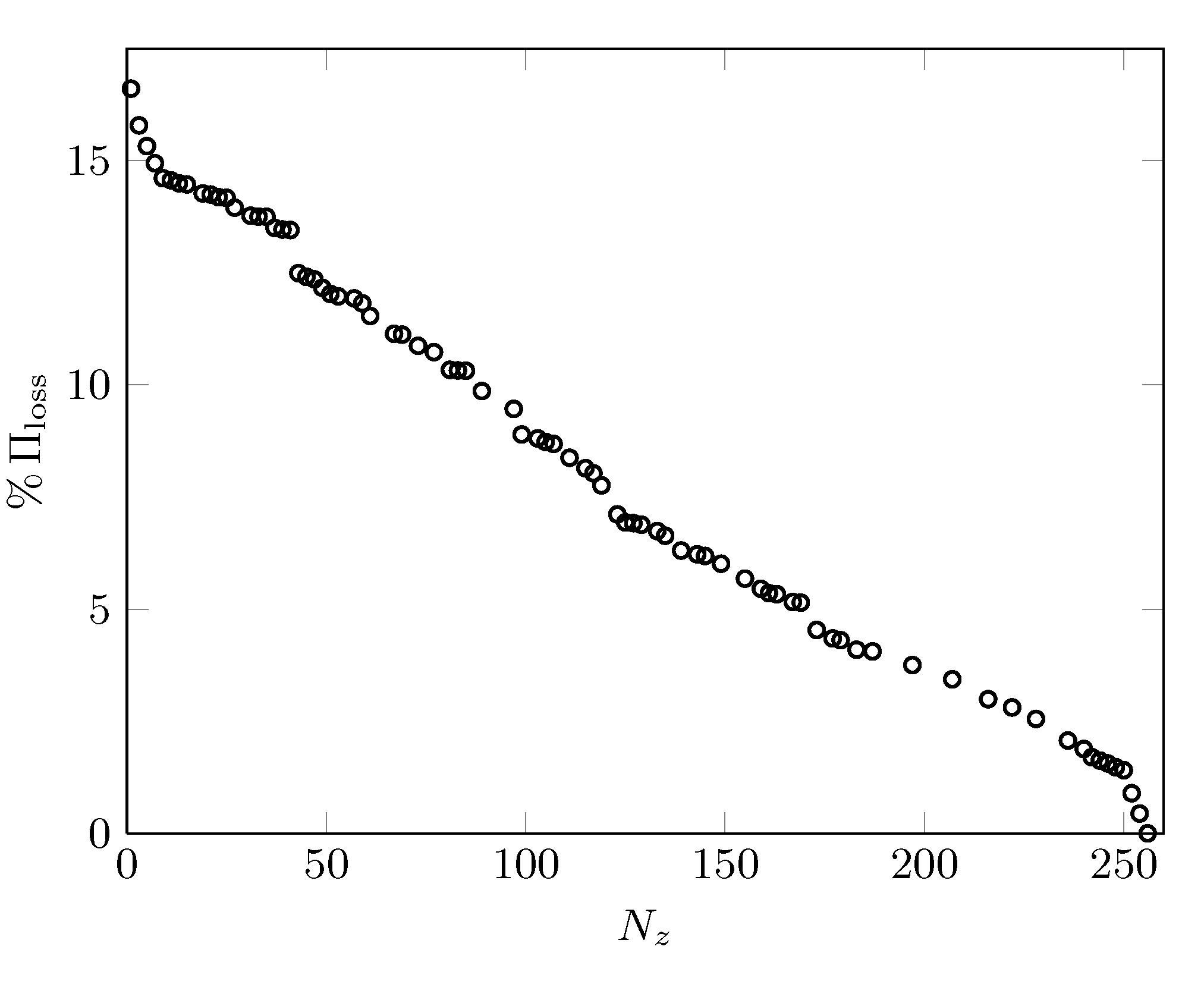 |
Performance loss,
|
Animation
This animation was generated by Joseph W. Nichols at the Center for Turbulence Research, Stanford University.
 and
and 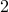 .
.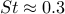 , the spectrum at location 2 (circles) is more broadbanded
than at location 1 (crosses).
, the spectrum at location 2 (circles) is more broadbanded
than at location 1 (crosses).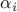 on (a)
the frequency and (b,c) the real part of the corresponding DMD
eigenvalues
on (a)
the frequency and (b,c) the real part of the corresponding DMD
eigenvalues 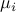 . Plot (c) represents a zoomed version of
plot (b) and it focuses on the amplitudes that correspond to lightly
damped eigenvalues.
. Plot (c) represents a zoomed version of
plot (b) and it focuses on the amplitudes that correspond to lightly
damped eigenvalues.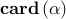 and (b) the
performance loss
and (b) the
performance loss
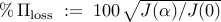 of the optimal vector of amplitudes
of the optimal vector of amplitudes 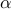 resulting from the
sparsity-promoting DMD algorithm.
resulting from the
sparsity-promoting DMD algorithm.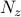 eigenvalues selected by the sparsity-promoting
DMD algorithm (crosses). In plots (b) and (c), the dashed curves
identify the unit circle.
eigenvalues selected by the sparsity-promoting
DMD algorithm (crosses). In plots (b) and (c), the dashed curves
identify the unit circle.