DMDSP – Sparsity-Promoting Dynamic Mode Decomposition
 |
Mihailo R. Jovanovic, Peter J. Schmid, Joseph W. Nichols September 2013 Matlab Files
Presentation
|
Purpose
This website provides a Matlab implementation of the Sparsity-Promoting
Dynamic Mode Decomposition (DMDSP) algorithm. Dynamic Mode Decomposition
(DMD) is an effective means for capturing the essential features of
numerically or experimentally generated snapshots, and its
sparsity-promoting variant DMDSP achieves a desirable tradeoff between
the quality of approximation (in the least-squares sense) and the number
of modes that are used to approximate available data. Sparsity is
induced by augmenting the least-squares deviation between the matrix of
snapshots and the linear combination of DMD modes with an additional
term that penalizes the 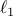 -norm of the vector of DMD amplitudes.
We employ alternating direction method of multipliers (ADMM) to solve
the resulting convex optimization problem and to efficiently compute the
globally optimal solution.
-norm of the vector of DMD amplitudes.
We employ alternating direction method of multipliers (ADMM) to solve
the resulting convex optimization problem and to efficiently compute the
globally optimal solution.
Problem formulation
Dynamic Mode Decomposition
Starting with a sequence of snapshots
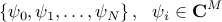
DMD provides a low-dimensional representation of a discrete-time linear time-invariant system
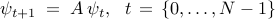
on a subspace spanned by the basis resulting from the Proper Orthogonal Decomposion (POD) of the data sequence. In particular, given two data matrices
![begin{array}{rcl} Psi_0 & = & left[ begin{array}{cccc} psi_0 & psi_1 & cdots & psi_{N-1} end{array} right] , in ; {bf C}^{M times N} [0.25cm] Psi_1 & = & left[ begin{array}{cccc} psi_1 & psi_2 & cdots & psi_{N} end{array} right] , in ; {bf C}^{M times N} end{array}](eqs/5084604633112247010-130.png)
the DMD algorithm provides optimal representation 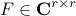 of the matrix
of the matrix 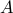 in the basis spanned by the POD modes of
in the basis spanned by the POD modes of
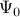 ,
,
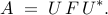
Here,  is the rank of the matrix of snapshots
is the rank of the matrix of snapshots 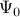 , and
, and
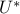 is the complex-conjugate-transpose of the matrix of POD modes
is the complex-conjugate-transpose of the matrix of POD modes
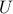 which is obtained from an economy-size singular value decomposition
(SVD) of
which is obtained from an economy-size singular value decomposition
(SVD) of 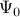 ,
,
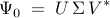
where 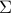 is an
is an  diagonal matrix determined by the
non-zero singular values
diagonal matrix determined by the
non-zero singular values  of
of  ,
and
,
and
![begin{array}{rcl} U , in , {bf C}^{M times r} & mbox{with} & U^* , U ; = ; I [0.25cm] V , in , {bf C}^{r times N} & mbox{with} & V^* , V ; = ; I. end{array}](eqs/9018660024346040480-130.png)
The matrix 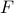 is determined from the matrices of snapshots
is determined from the matrices of snapshots 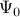 and
and
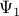 by minimizing the Frobenius norm of the difference between
by minimizing the Frobenius norm of the difference between
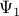 and
and 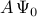 , thereby resulting into
, thereby resulting into
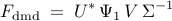
Optimal amplitudes of DMD modes
The matrix 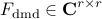 determines an
optimal low-dimensional representation of the inter-snapshot mapping
determines an
optimal low-dimensional representation of the inter-snapshot mapping 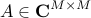 on the subspace spanned by the POD modes of
on the subspace spanned by the POD modes of
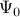 . The dynamics on this
. The dynamics on this  -dimensional subspace are governed by
-dimensional subspace are governed by
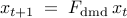
and the matrix of POD modes 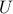 can be used to map
can be used to map 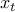 into a
higher dimensional space
into a
higher dimensional space 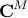 ,
,
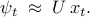
If 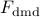 has a full set of linearly independent eigenvectors
has a full set of linearly independent eigenvectors  , with corresponding eigenvalues
, with corresponding eigenvalues  , then it can be brought into a diagonal coordinate form and
experimental or numerical snapshots can be approximated using a
linear combination of DMD modes,
, then it can be brought into a diagonal coordinate form and
experimental or numerical snapshots can be approximated using a
linear combination of DMD modes,
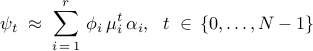
or, equivalently, in matrix form,
![overbrace{ left[ begin{array}{cccc} psi_0 & psi_1 & cdots & psi_{N-1} end{array} right] }^{Psi_0} ~ approx ~ overbrace{ left[ begin{array}{cccc} phi_1 & phi_2 & cdots & phi_{r} end{array} right] }^{Phi} , overbrace{ left[ begin{array}{cccc} alpha_1 & & & & alpha_2 & & & & ddots & & & & alpha_r end{array} right] }^{D_{alpha} ; mathrel{mathop:}= ~ hbox{diag} , { alpha }} , overbrace{ left[ begin{array}{cccc} 1 & mu_1 & cdots & mu_1^{N-1} [0.15cm] 1 & mu_2 & cdots & mu_2^{N-1} vdots & vdots & ddots & vdots [0.15cm] 1 & mu_r & cdots & mu_r^{N-1} end{array} right] }^{V_{mathrm{and}}}.](eqs/1855197274586821425-130.png)
Here, the matrix of POD modes 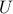 and the matrix of eigenvectors of
and the matrix of eigenvectors of 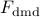 ,
,
![Y mathrel{mathop:}= left[ begin{array}{ccc} y_1 & cdots & y_r end{array} right],](eqs/2512904103656975035-130.png) are used to determine the matrix of DMD modes
are used to determine the matrix of DMD modes
![Phi ; = , left[ begin{array}{ccc} phi_1 & cdots & phi_r end{array} right] , = ; U , Y , in , {bf C}^{M times r}.](eqs/788263300204692144-130.png)
Furthermore, the amplitude 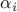 quantifies the
quantifies the 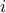 th modal
contribution of the initial condition
th modal
contribution of the initial condition 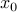 on the subspace spanned by
the POD modes of
on the subspace spanned by
the POD modes of 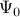 , and the temporal evolution of the dynamic
modes is governed by the Vandermonde matrix
, and the temporal evolution of the dynamic
modes is governed by the Vandermonde matrix 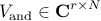 which is determined by the
which is determined by the  eigenvalues
eigenvalues 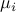 of
of
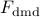 .
.
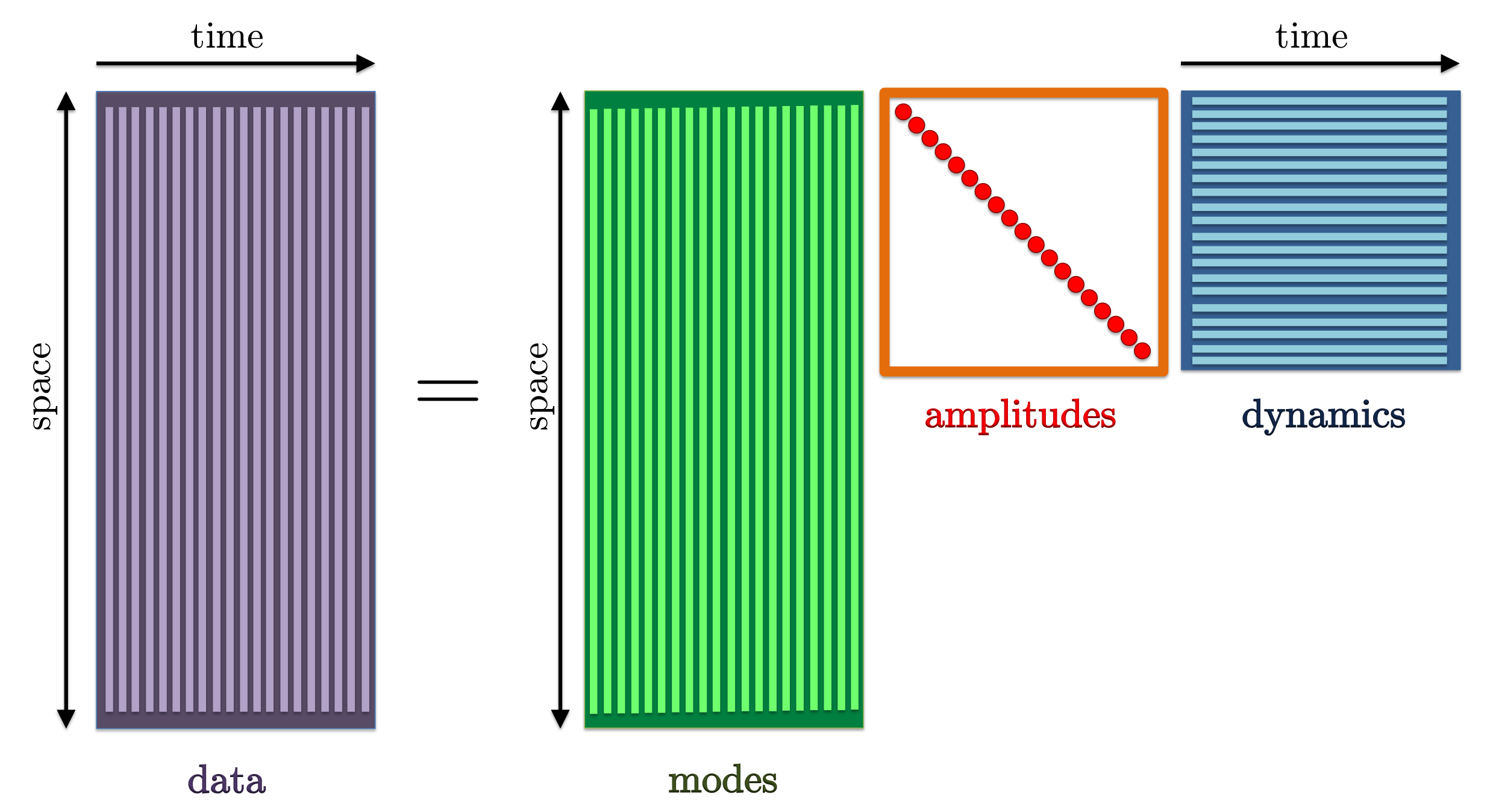 |
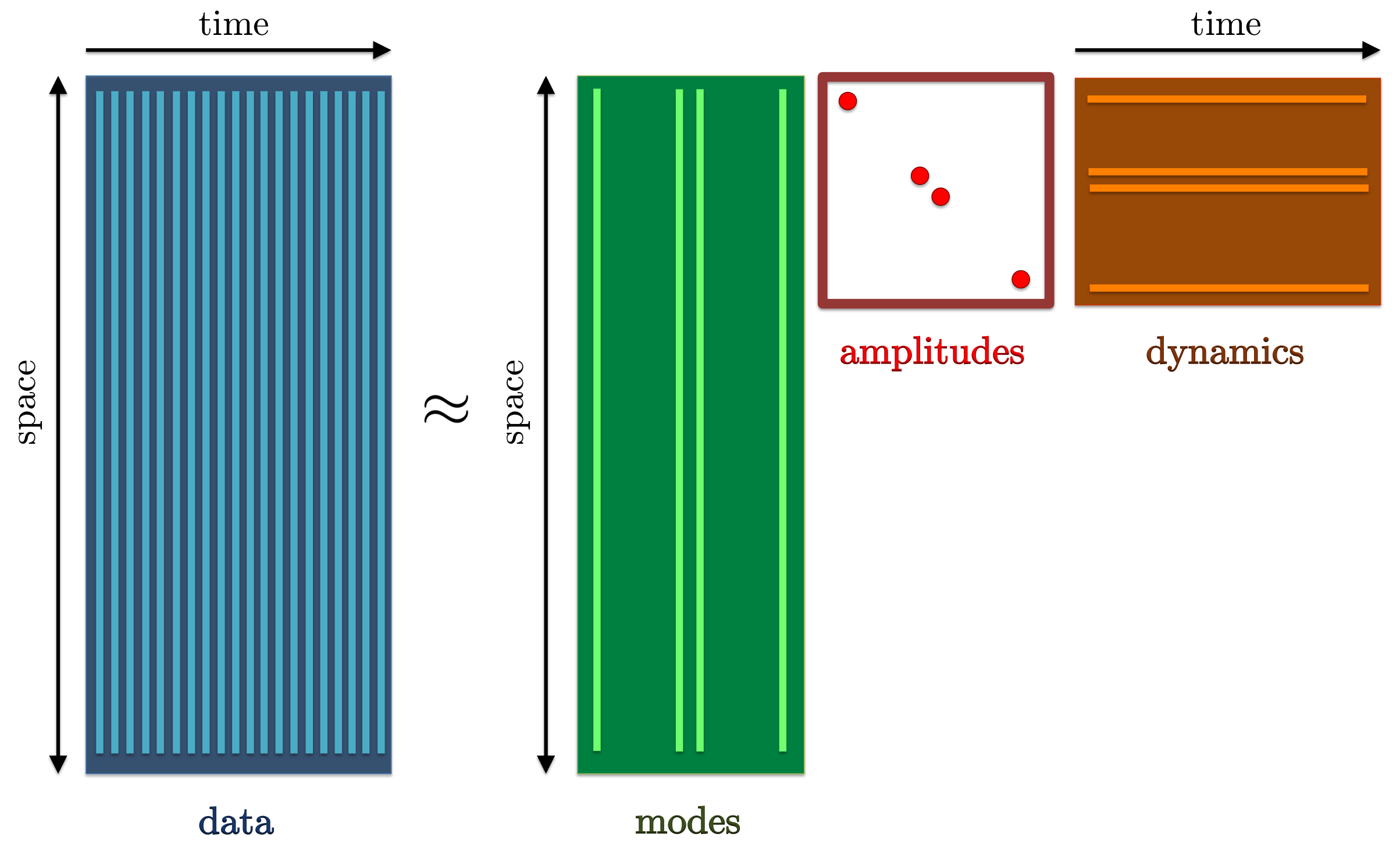
Dynamic mode decomposition can be used to represent experimentally or numerically generated snapshots as a linear combination of DMD modes, properly weighted by their amplitudes and advanced in time according to their temporal growth/decay rate. |
Determination of the optimal vector of amplitudes
![alpha mathrel{mathop:}= left[ begin{array}{ccc} alpha_1 & cdots & alpha_r end{array} right]^T](eqs/8325933437344555517-130.png) then amounts to minimization of the Frobenius norm of the difference
between
then amounts to minimization of the Frobenius norm of the difference
between 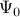 and
and 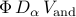 . Using SVD
of
. Using SVD
of 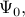 the definition of the matrix
the definition of the matrix 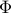 , and a sequence of
straightforward algebraic manipulations, this convex optimization
problem can be brought into the following form
, and a sequence of
straightforward algebraic manipulations, this convex optimization
problem can be brought into the following form
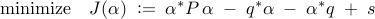
where 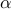 is the optimization variable and the problem data is
determined by
is the optimization variable and the problem data is
determined by

Here, an asterisk denotes the complex-conjugate-transpose of a vector
(matrix), an overline signifies the complex-conjugate of a vector
(matrix), 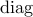 of a vector is a diagonal matrix with its main
diagonal determined by the elements of a given vector,
of a vector is a diagonal matrix with its main
diagonal determined by the elements of a given vector, 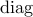 of a
matrix is a vector determined by the main diagonal of a given matrix,
and
of a
matrix is a vector determined by the main diagonal of a given matrix,
and  is the elementwise multiplication of two matrices.
is the elementwise multiplication of two matrices.
The optimal vector of DMD amplitudes that minimizes
the Frobenius norm of the difference between
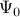 and
and 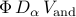 can thus be obtained by minimizing the quadratic function
can thus be obtained by minimizing the quadratic function 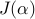 with respect to
with respect to 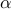 ,
,
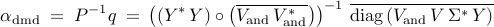
Sparsity-promoting dynamic mode decomposition
We now direct our attention to the problem of selecting the subset of DMD modes that has the most profound influence on the quality of approximation of a given sequence of snapshots. In the first step, we seek a sparsity structure that achieves a user-defined tradeoff between the number of extracted modes and the approximation error (with respect to the full data sequence). In the second step, we fix the sparsity structure of the vector of amplitudes (identified in the first step) and determine the optimal values of the non-zero amplitudes.
 |
The sparsity-promoting dynamic mode decomposition is aimed at identifying a subset of DMD modes that optimally approximate the entire data sequence. |
We approach the problem of inducing sparsity by augmenting the objective function
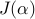 with an additional term that penalizes the
the
with an additional term that penalizes the
the 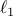 -norm of the vector of unknown amplitudes
-norm of the vector of unknown amplitudes 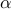 ,
,
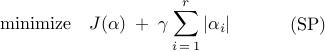
In the modified optimization problem (SP), 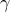 is a positive
regularization parameter that reflects our emphasis on sparsity of the
vector
is a positive
regularization parameter that reflects our emphasis on sparsity of the
vector 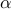 . Larger values of
. Larger values of 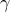 place stronger emphasis on
the number of non-zero elements in the vector
place stronger emphasis on
the number of non-zero elements in the vector 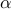 (relative to the
quality of the least-squares approximation,
(relative to the
quality of the least-squares approximation, 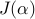 ), thereby
encouraging sparser solutions.
), thereby
encouraging sparser solutions.
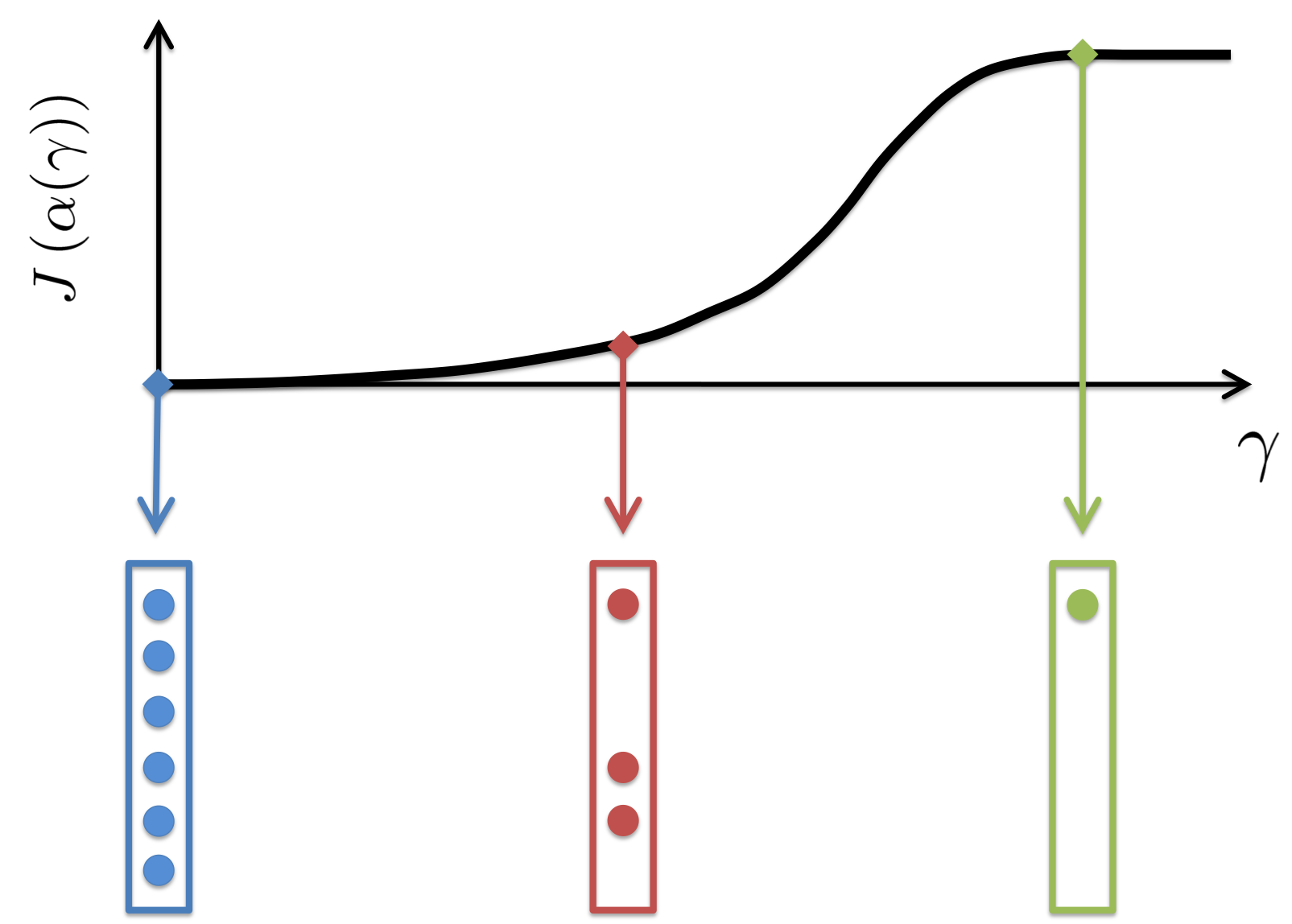 |
Increased emphasis on sparsity encourages sparser solutions at the expense of compromising quality of least-squares approximation. |
After a desired balance between the quality of approximation of experimental or numerical snapshots and the number of DMD modes is achieved, we fix the sparsity structure of the unknown vector of amplitudes and determine only the non-zero amplitudes as the solution to the following constrained convex optimization problem:
![begin{array}{cc} begin{array}{rl} {rm minimize} & J (alpha) [0.25cm] {rm subject~to} & E^T , alpha , = , 0 end{array} & hspace{1.cm} {rm (POL)} end{array}](eqs/4683364808033973736-130.png)
Here, the matrix 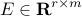 encodes information about
the sparsity structure of the vector
encodes information about
the sparsity structure of the vector  . The columns of
. The columns of  are
the unit vectors in
are
the unit vectors in 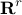 whose non-zero elements correspond to
zero components of
whose non-zero elements correspond to
zero components of 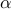 . For example, for
. For example, for 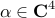 with
with
![alpha ; = , left[ begin{array}{cccc} alpha_1 & 0 & alpha_3 & 0 end{array} right]^T](eqs/6780487391022173678-130.png)
the matrix 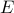 is given as
is given as
![E ; = , left[ begin{array}{cc} 0 & 0 1 & 0 0 & 0 0 & 1 end{array} right].](eqs/6443431621411358696-130.png)
Alternating direction method of multipliers (ADMM)
ADMM is a simple but powerful algorithm well-suited to large optimization problems. In the sparsity-promoting DMD problem, the algorithm consists of four steps:
Step 1: introduce additional variable/constraint
![begin{array}{ll} {rm minimize} & J(alpha) ; + ; gamma , g (beta) [0.25cm] {rm subject~to} & alpha ; - ; beta ; = ; 0 end{array}](eqs/2363429738284218855-130.png)
Step 2: introduce the augmented Lagrangian
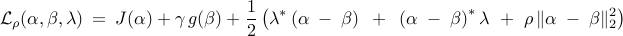
Step 3: use ADMM for the augmented Lagrangian minimization
![begin{array}{rllll} bf{alpha !! - !! minimization~problem:} && alpha^{k+1} & !! mathrel{mathop:}= !! & {displaystyle {rm arg , min}_{alpha}} ; {cal L}_rho (alpha,beta^k,lambda^k) [0.35cm] bf{beta !! - !! minimization~problem:} && beta^{k+1} & !! mathrel{mathop:}= !! & {displaystyle {rm arg , min}_{beta}} ; {cal L}_rho (alpha^{k+1},beta,lambda^k) [0.35cm] bf{lambda !! - !! update~step:} && lambda^{k+1} & !! mathrel{mathop:}= !! & lambda^{k} ;+; rho left( alpha^{k+1} ; - ; beta^{k+1} right) end{array}](eqs/3466259005028321646-130.png)
Step 4: polishing - solve the structured quadratic programming problem for the identified sparsity pattern
![{bf structured~optimization~problem}!!: ~~ left{ begin{array}{ll} {rm minimize} & J(alpha) [0.2cm] {rm subject~to} & E^T , alpha , = , 0 end{array} right.](eqs/7599470449733391662-130.png)
Solution to (SP)
The respective structures of the functions 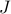 and
and 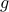 in the
sparsity-promoting DMD problem can be exploited to show that the
in the
sparsity-promoting DMD problem can be exploited to show that the
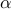 -minimization step amounts to solving an unconstrained
regularized quadratic program and that the
-minimization step amounts to solving an unconstrained
regularized quadratic program and that the 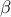 -minimization step
amounts to a use of the soft thresholding operator
-minimization step
amounts to a use of the soft thresholding operator 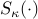 :
:
![begin{array}{rllll} bf{alpha !! - !! minimization~problem:} && alpha^{k+1} & !! = !! & left( P , + , (rho/2) , I right)^{-1} left( q , + , (rho/2) left( beta^k ; - ; ( 1/rho ) , lambda^k right) right) [0.35cm] bf{beta !! - !! minimization~problem:} && beta_i^{k+1} & !! = !! & S_{kappa} ( alpha_i^{k+1} ; + , left( 1/rho right) lambda_i^k ), ~~ kappa ; = ; gamma/rho, ~~ i ; = ; left{ 1, ldots, r right} [0.35cm] bf{lambda !! - !! update~step:} && lambda^{k+1} & !! = !! & lambda^{k} ;+; rho left( alpha^{k+1} ; - ; beta^{k+1} right) end{array}](eqs/5852205348158191612-130.png)
where
![S_kappa (v_i^k) ; mathrel{mathop:}= ; left{ begin{array}{ll} v_i^k ,-, kappa, & v_i^k , > , kappa [0.15cm] 0, & v_i^k , in , [ -kappa, , kappa ] [0.15cm] v_i^k ,+, kappa, & v_i^k , < , -kappa end{array} right.](eqs/7179891368550501809-130.png)
Solution to (POL)
After the desired sparsity structure has been identified, the
optimal vector of amplitudes with a fixed sparsity structure,
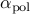 , can be determined from:
, can be determined from:
![alpha_{mathrm{pol}} ; = ; left[ begin{array}{cc} {I} & {0} end{array} right] left[ begin{array}{cc} {P} & {E} [0.05cm] {E^T} & {0} end{array} right]^{-1} left[ begin{array}{c} {q} [0.1cm] {0} end{array} right]](eqs/5969431933168193388-130.png)
Acknowledgments
We gratefully acknowledge Prof. Parviz Moin for his encouragement to pursue this effort during the 2012 Center for Turbulence Research Summer Program at Stanford University.