% Sparsity-Promoting Dynamic Mode Decomposition (DMDSP) % % Written by Mihailo R. Jovanovic, August 2012 % % The alternating direction method of multipliers (ADMM) % is used to solve the sparsity-promoting DMD problem: % % minimize J(x) + gamma * || x ||_1 (SP) % % J(x) = || G - L diag{x} R ||_F^2 % % complex-valued data G, L, R; optimization variable x % % J(x) can be equivalently written as % J(x) = x'*P*x - 2*real(q'*x) + s % % P = (L'*L).*conjugate(R*R') % q = conjugate(diag(R*G'*L)) % s = trace(G'*G) % % For the identified sparsity pattern, the optimal vector of % amplitudes is found as the answer to the following % structured quadratic optimization problem: % % minimize J(x) % (POL) % subject to E'*x = 0 % % where the columns of the matrix E are the unit vectors % whose non-zero elements correspond to zero components of x % % Syntax: % % answer = dmdsp(P,q,s,gammaval,options) % % Inputs: (1) matrix P % vector q % scalar s % sparsity promoting parameter gamma % % (2) options % % options.rho - augmented Lagrangian parameter rho % options.maxiter - maximum number of ADMM iterations % options.eps_abs - absolute tolerance % options.eps_rel - relative tolerance % % If options argument is omitted, the default values are set to % % options.rho = 1 % options.maxiter = 10000 % options.eps_abs = 1.e-6 % options.eps_rel = 1.e-4 % % Output: answer - gamma-parameterized structure containing % % answer.gamma - sparsity-promoting parameter gamma % answer.xsp - vector of amplitudes resulting from (SP) % answer.xpol - vector of amplitudes resulting from (POL) % answer.Jsp - J resulting from (SP) % answer.Jpol - J resulting from (POL) % answer.Nz - number of nonzero elements of x % answer.Ploss - optimal performance loss 100*sqrt(J(xpol)/J(0)) % % Additional information: % % http://www.umn.edu/~mihailo/software/dmdsp/ function answer = dmdsp(P,q,s,gammaval,options) % Initialization if nargin < 4 error('At least four input arguments are required.') elseif nargin == 4 options = struct('rho',1,'maxiter',10000,'eps_abs',1.e-6,'eps_rel',1.e-4); elseif nargin > 5 error('Too many input arguments.') end % Data preprocessing rho = options.rho; Max_ADMM_Iter = options.maxiter; eps_abs = options.eps_abs; eps_rel = options.eps_rel; % Number of optimization variables n = length(q); % Identity matrix I = eye(n); % Allocate memory for gamma-dependent output variables answer.gamma = gammaval; answer.Nz = zeros(1,length(gammaval)); % number of non-zero amplitudes answer.Jsp = zeros(1,length(gammaval)); % square of Frobenius norm (before polishing) answer.Jpol = zeros(1,length(gammaval)); % square of Frobenius norm (after polishing) answer.Ploss = zeros(1,length(gammaval)); % optimal performance loss (after polishing) answer.xsp = zeros(n,length(gammaval)); % vector of amplitudes (before polishing) answer.xpol = zeros(n,length(gammaval)); % vector of amplitudes (after polishing) % Cholesky factorization of matrix P + (rho/2)*I Prho = (P + (rho/2)*I); Plow = chol(Prho,'lower'); Plow_star = Plow'; for i = 1:length(gammaval), gamma = gammaval(i); % Initial conditions y = zeros(n,1); % Lagrange multiplier z = zeros(n,1); % copy of x % Use ADMM to solve the gamma-parameterized problem for ADMMstep = 1 : Max_ADMM_Iter, % x-minimization step u = z - (1/rho)*y; % x = (P + (rho/2)*I)\(q + (rho)*u) xnew = Plow_star\(Plow\(q + (rho/2)*u)); % z-minimization step a = (gamma/rho)*ones(n,1); v = xnew + (1/rho)*y; % Soft-thresholding of v znew = ( (1 - a ./ abs(v)) .* v ) .* (abs(v) > a); % Primal and dual residuals res_prim = norm(xnew - znew); res_dual = rho * norm(znew - z); % Lagrange multiplier update step y = y + rho*(xnew - znew); % Stopping criteria eps_prim = sqrt(n) * eps_abs + eps_rel * max([norm(xnew),norm(znew)]); eps_dual = sqrt(n) * eps_abs + eps_rel * norm(y); if (res_prim < eps_prim) && (res_dual < eps_dual) break; else z = znew; end end % Record output data answer.xsp(:,i) = z; % vector of amplitudes answer.Nz(i) = nnz(answer.xsp(:,i)); % number of non-zero amplitudes answer.Jsp(i) = real(z'*P*z) - 2*real(q'*z) + s; % Frobenius norm (before polishing) % Polishing of the nonzero amplitudes % Form the constraint matrix E for E^T x = 0 ind_zero = find( abs(z) < 1.e-12); % find indices of zero elements of z m = length(ind_zero); % number of zero elements E = I(:,ind_zero); E = sparse(E); % Form KKT system for the optimality conditions KKT = [P, E; E', zeros(m,m)]; rhs = [q; zeros(m,1)]; % Solve KKT system sol = KKT \ rhs; % Vector of polished (optimal) amplitudes xpol = sol(1:n); % Record output data answer.xpol(:,i) = xpol; % Polished (optimal) least-squares residual answer.Jpol(i) = real(xpol'*P*xpol) - 2*real(q'*xpol) + s; % Polished (optimal) performance loss answer.Ploss(i) = 100*sqrt(answer.Jpol(i)/s); end
Description of dmdsp.m
>> answer = dmdsp(P,q,s,gammaval,options);
Matlab function dmdsp.m takes the problem data
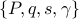 and the input options and returns the
and the input options and returns the 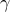 -parameterized family of
solutions to both the sparsity-promoting DMD problem (SP) and the
constrained quadratic optimization problem (POL). Input options allows
users to specify the following parameters
-parameterized family of
solutions to both the sparsity-promoting DMD problem (SP) and the
constrained quadratic optimization problem (POL). Input options allows
users to specify the following parameters
options.rho – augmented Lagrangian parameter
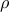 ;
;options.maxiter – maximum number of ADMM iterations;
options.eps_abs – absolute tolerance;
options.eps_rel – relative tolerance.
If options argument is omitted, the default values are set to:
options.rho = 1;
options.maxiter = 10000;
options.eps_abs = 1.e-6;
options.eps_rel = 1.e-4;
The 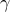 -parameterized output answer is a structure that contains
-parameterized output answer is a structure that contains
answer.gamma – sparsity-promoting parameter
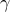
answer.xsp – vector of amplitudes
 resulting from the optimization problem (SP);
resulting from the optimization problem (SP);answer.xpol – optimal (polished) vector of amplitudes
 resulting from the
structured quadratic optimization problem (POL);
resulting from the
structured quadratic optimization problem (POL);answer.Jsp – least-squares residual resulting from the optimization problem (SP);
answer.Jpol – optimal (polished) least-squares residual resulting from the optimization problem (POL);
answer.Ploss – optimal (polished) performance loss
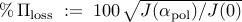 ;
;answer.Nz – number of nonzero elements in the vector of amplitudes
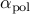 .
.