% System parameters: omval = logspace(5,7,300); % temporal frequencies % beam parameters alpha = 5e-8; mu = 1.88e-7; ell = 240e-6; EI = 7.55e-12; % convenience variables a4 = EI/(ell^4); a3 = EI/(ell^3); dom = domain(0,1); % domain, y \in [0, 1] y = chebfun('y',dom); D1 = diff(dom,1); % first-order differentiation operator % fone(y) = 1; fzero(y) = 0; fone = chebfun(1,dom); fzero = chebfun(0,dom); % Boundary conditions on the right end: Wa = [1, 0, 0, 0; 0, 1, 0, 0; zeros(2,4)]; r = [0; 0; 0; (1/a3)]; % non-homogeneous boundary conditions % Computing frequency responses H1 = zeros(length(omval),1); KE = zeros(length(omval),1); PE = zeros(length(omval),1); for indom = 1:length(omval) om = omval(indom); % boundary conditions on the left end Wb = [zeros(2,4); ... 0, 0, 1, 0; ... 0, 0, 0, (1 + alpha*1i*om)]; % system coefficients A0 = [-mu*om*om*fone, fzero, fzero, fzero, a4*(1 + alpha*1i*om)*fone]; % solving integral boundary value problem % intbvp solves a scalar boundary value problem using the integral % representation % (type 'help intbvp' for more information on how to use intbvp) % intbvp.m is included in the download zip-folder [f,fder] = intbvp(A0,fzero,Wa,Wb,r); % frequency responses % 1) with the output g(t) = phi(1,t) = f(1,t) H1(indom) = f(1); % 2) with the output f(y,t) = phi(y,t) % kinetic energy: KE = 0.5*integrate_{0}^{1} (f??(y))^2 dy KE(indom) = 0.5*norm(D1*D1*f)^2; % potential energy: PE = 0.5*om*om*integrate_{0}^{1} f(y)^2 dy PE(indom) = 0.5*norm(om*f)^2; end % total energy: TE = PE + KE TE = KE + PE;
Boundary actuation: an Euler-Bernoulli beam
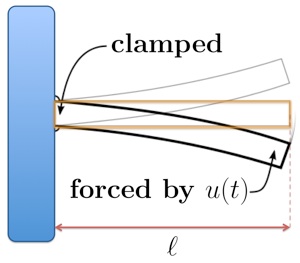 |
The vertical displacement of an Euler-Bernoulli beam that is clamped at the left end and subject to a boundary actuation at the other end is governed by
![begin{array}{rcl} mu , phi_{tt} (y, t) , + , {displaystyle frac{alpha , E_{I}}{ell^{4}}} , phi_{tyyyy}(y,t) , + , {displaystyle frac{E_{I}}{ell^{4}}} , phi_{yyyy}(y,t) & !! = !! & 0, ;; y in left[ , 0, 1 , right] [0.5cm] phi(0, t) ; = ; phi_{y}(0, t) & !! = !! & 0 [0.4cm] phi_{yy}( 1, t ) ; = ; 0, ;;; {displaystyle frac{alpha , E_{I}}{ell^{3}}} , phi_{tyyy}(1, t) , + , {displaystyle frac{E_{I}}{ell^{3}}} , phi_{yyy}(1, t) & !! = !! & u(t) end{array}](eqs/6526122142977153027-130.png)
where
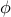 | — | vertical displacement of the beam |
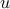 | — | force acting on the tip |
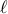 | — | length of the beam |
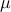 | — | mass per unit length of the beam |
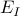 | — | flexural stiffness |
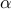 | — | Voigt damping factor. |
The outputs are given by
![begin{array}{rcl} g (t) & !! = !! & phi(1,t) [0.15cm] f (y, t) & !! = !! & phi(y, t). end{array}](eqs/2673647037006230887-130.png)
Application of the temporal Fourier transform yields
![begin{array}{rcl} left( {displaystyle frac{E_{I}}{ell^{4}} left( 1 , + , mathrm{i} , omega , alpha right) D^{(4)} , - , omega^2 , mu } right) , phi (y, omega) & !! = !! & 0 [0.45cm] phi(0, omega) ; = ; D^{(1)} , phi(0, omega) & !! = !! & 0 [0.25cm] D^{(2)} , phi( 1, omega) ; = ; 0, ;;; {displaystyle frac{E_{I}}{ell^{3}} left( 1 , + , mathrm{i} , omega , alpha right) } , D^{(3)} , phi(1, omega) & !! = !! & u(omega). end{array}](eqs/3619645815926670013-130.png)
Matlab codes
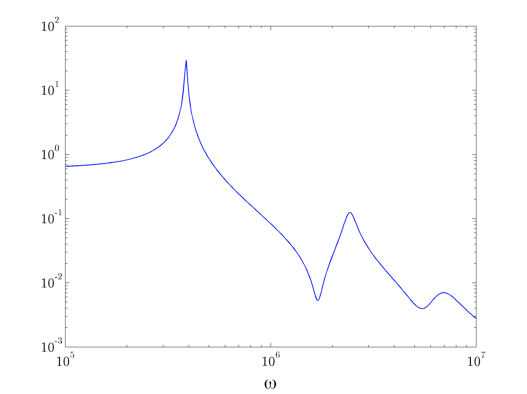
Plot the magnitude and phase of the transfer function from 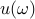 to
to 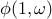 .
.
loglog(omval,abs(H1),'b-','LineWidth',1.1) xlab = xlabel('\omega', 'interpreter', 'tex'); set(xlab, 'FontName', 'cmmi10', 'FontSize', 20); h = get(gcf,'CurrentAxes'); set(h, 'FontName', 'cmr10', 'FontSize', 15); semilogx(omval,unwrap(angle(H1)),'b-','LineWidth',1.1) xlab = xlabel('\omega', 'interpreter', 'tex'); set(xlab, 'FontName', 'cmmi10', 'FontSize', 20); h = get(gcf,'CurrentAxes'); set(h, 'FontName', 'cmr10', 'FontSize', 15);
 |
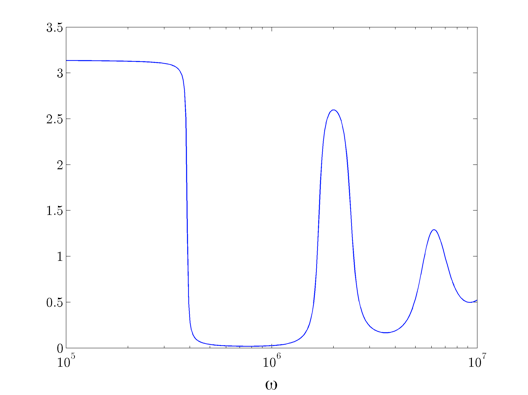 |
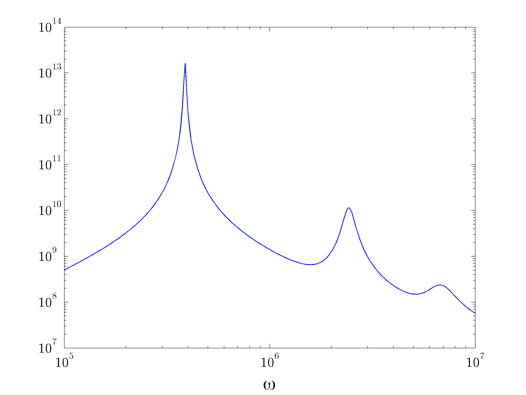
Plot the total energy of the beam arising from boundary actuation.
loglog(omval,TE,'b-','LineWidth',1.1) xlab = xlabel('\omega', 'interpreter', 'tex'); set(xlab, 'FontName', 'cmmi10', 'FontSize', 20); h = get(gcf,'CurrentAxes'); set(h, 'FontName', 'cmr10', 'FontSize', 15);
 |