% System parameters: R = 2000; % Reynolds number kxval = linspace(0.1,5,100); % streamwise wave-number kxgrd = length(kxval); om = -0.3; % temporal frequency dom = domain(-1,1); % domain of your function y = chebfun('y',dom); fone = chebfun(1,dom); % fone(y) = 1 fzero = chebfun(0,dom); % fzero(y) = 0 U = diag(1 - y.^2); % in pressure-driven flow Uy = diag(-2*y); Uyy = diag(-2*fone); % Boundary conditions Wa0{1} = [1, 0, 0, 0; 0, 1, 0, 0]; Wb0{1} = [1, 0, 0, 0; 0, 1, 0, 0]; % Looping over different values of kx Smax = zeros(kxgrd,1); A0 = cell(1,1); B0 = cell(1,2); C0 = cell(2,1); for indx = 1:kxgrd kx = kxval(indx); kx2 = kx*kx; kx4 = kx2*kx2; % coefficients of the A0 operator % a0*phi + 0*phi' + a2*phi'' + 0*phi''' + 1/R*phi'''' a2 = -(2*kx2*(1/R)*fone + 1i*kx*U*fone + 1i*om*fone); a0 = (1/R)*kx4*fone + 1i*kx*kx2*U*fone + 1i*kx*Uyy*fone + ... 1i*om*kx2*fone; A0{1} = [a0, fzero, a2, fzero, (1/R)*fone]; % coefficients of the B0 operator % 0*d1 - d1' + i*kx*d2 + 0*d2' B0{1,1} = [fzero, -fone]; B0{1,2} = [1i*kx*fone, fzero]; % coefficients of the C0 operator % u = 0*phi + 1*phi'; v = -i*kx*phi + 0*phi' C0{1,1} = [fzero, fone]; C0{2,1} = [-1i*kx*fone, fzero]; % solving for the left principal singular pair [Sfun, Sval] = svdfr(A0,B0,C0,Wa0,Wb0,1,1); % saving the largest singular value at each kx Smax(indx) = Sval(1); end % Plotting the largest singular value as a function of kx at a fixed om plot(kxval,Smax,'-','LineWidth',1.1); xlab = xlabel('k_x', 'interpreter', 'tex'); set(xlab, 'FontName', 'cmmi10', 'FontSize', 20); h = get(gcf,'CurrentAxes'); set(h,'FontName','cmr10','FontSize',15,'xscale','log','yscale','lin');
Two-dimensional channel flow
(Orr-Sommerfeld operator)
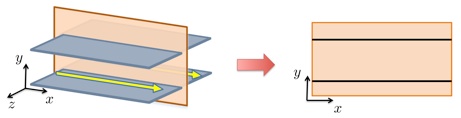 |
Two-dimensional channel flow geometry. |
The Orr-Sommerfeld equation governs the dynamics of two-dimensional velocity fluctuations around the laminar channel flow,
![begin{array}{rcl} Delta phi_{t} (k_x, y, t) & !! = !! & left( {displaystyle frac{1}{R}} Delta^{2} , - , mathrm{i} , k_x , U(y) , Delta , + , mathrm{i} , k_x , U''(y) right) phi(k_x, y, t) [0.3cm] & & + , D^{(1)} , d_{1}(k_x, y, t) , - , mathrm{i} , k_x , d_{2}(k_x, y, t), ;;; y in left[ -1, 1 right] end{array}](eqs/8905391176719166528-130.png)
where
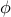 | — | streamfunction |
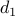 , , 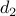 | — | streamwise and wall-normal forcing |
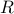 | — | Reynolds number |
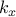 | — | streamwise wavenumber |
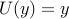 | — | for shear-driven flow |
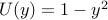 | — | for pressure-driven flow |
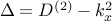 | — | Laplacian |
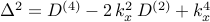 . . | ||
The boundary conditions are given by
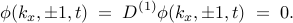
The desired outputs are the streamwise and wall-normal velocity fluctuations,
![begin{array}{rcl} u(k_x, y, t) & !! = !! & D^{(1)} , phi(k_x, y, t) [0.15cm] v(k_x, y, t) & !! = !! & -mathrm{i} , k_x , phi(k_x, y, t). end{array}](eqs/6403025569654224186-130.png)
The input-output differential equation representing the frequency response operator is given by
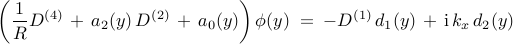
where
![begin{array}{rcl} a_{2}(y) & !! = !! & {displaystyle -left( frac{2 , k_x^2}{R} , + , mathrm{i}, k_x , U(y) , + , mathrm{i} , omega right)} [0.4cm] a_{0}(y) & !! = !! & {displaystyle frac{k_x^{4}}{R}} , + , mathrm{i} , k_x^3 , U(y) , + , mathrm{i} , k_x , U''(y) , + , mathrm{i} , omega , k_x^2. end{array}](eqs/1066555399194103489-130.png)
Matlab codes
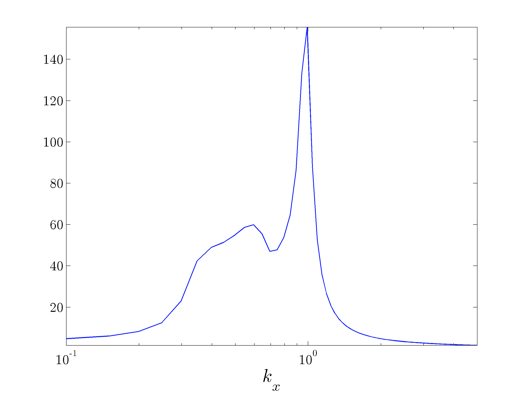
Find the largest singular value of the frequency response operator for the Orr-Sommerfeld equation
in a pressure-driven channel flow as a function of 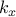 at
at 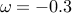 .
.
 |
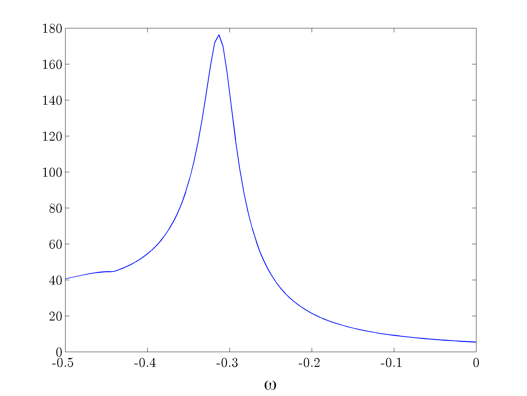
Find the largest singular value of the frequency response operator for the Orr-Sommerfeld equation
in a pressure-driven channel flow as a function of 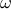 at
at 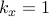 .
.
% the OS-equation as a function of om at kx = 1. % System parameters: kx = 1; % streamwise wave-number kx2 = kx*kx; kx4 = kx2*kx2; omval = linspace(-0.5,0,100); % temporal frequency omgrd = length(omval); % Looping over different values of om Smax = zeros(omgrd,1); A0 = cell(1,1); B0 = cell(1,2); C0 = cell(2,1); for indom = 1:omgrd om = omval(indom); % coefficients of the A0 operator % a0*phi + 0*phi' + a2*phi'' + 0*phi''' + 1/R*phi'''' a2 = -(2*kx2*(1/R)*fone + 1i*kx*U*fone + 1i*om*fone); a0 = (1/R)*kx4*fone + 1i*kx*kx2*U*fone + 1i*kx*Uyy*fone + ... 1i*om*kx2*fone; A0{1} = [a0, fzero, a2, fzero, (1/R)*fone]; % coefficients of the B0 operator % 0*d1 - 1*d1' + i*kx*d2 + 0*d2' B0{1,1} = [fzero, -fone]; B0{1,2} = [1i*kx*fone, fzero]; % coefficients of the C0 operator % u = 0*phi + 1*phi'; v = -i*kx*phi + 0*phi' C0{1,1} = [fzero, fone]; C0{2,1} = [-1i*kx*fone, fzero]; % solving for the left principal singular pair [Sfun, Sval] = svdfr(A0,B0,C0,Wa0,Wb0,1,1); % saving the largest singular value for each value of om Smax(indom) = Sval(1); end % Plotting the largest singular value as a function of om at a fixed kx plot(omval,Smax,'-','LineWidth',1.1); xlab = xlabel('\omega', 'interpreter', 'tex'); set(xlab, 'FontName', 'cmmi10', 'FontSize', 20); h = get(gcf,'CurrentAxes'); set(h,'FontName','cmr10','FontSize',15,'xscale','lin','yscale','lin');
 |
Find the most amplified flow structures for the Orr-Sommerfeld equation in a pressure-driven channel flow
at 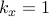 and
and 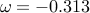 .
.
% System parameters: kxval = [1 -1]; % streamwise wave-number omval = 0.313*[-1 1]; % temporal frequency N = 100; % number of collocation points for plotting yd = chebpts(N); % Looping over different values of om and kx A0 = cell(1,1); B0 = cell(1,2); C0 = cell(2,1); for n = 1:2 om = omval(n); kx = kxval(n); kx2 = kx*kx; kx4 = kx2*kx2; % coefficients of the A0 operator % a0*phi + 0*phi' + a2*phi'' + 0*phi''' + 1/R*phi'''' a2 = -(2*kx2*(1/R)*fone + 1i*kx*U*fone + 1i*om*fone); a0 = (1/R)*kx4*fone + 1i*kx*kx2*U*fone + 1i*kx*Uyy*fone + ... 1i*om*kx2*fone; A0{1} = [a0, fzero, a2, fzero, (1/R)*fone]; % coefficients of the B0 operator % 0*d1 - 1*d1' + i*kx*d2 + 0*d2' B0{1,1} = [fzero, -fone]; B0{1,2} = [1i*kx*fone, fzero]; % coefficients of the C0 operator % u = 0*phi + 1*phi'; v = -i*kx*phi + 0*phi' C0{1,1} = [fzero, fone]; C0{2,1} = [-1i*kx*fone, fzero]; % solving for the left principal singular pair [Sfun, Sval] = svdfr(A0,B0,C0,Wa0,Wb0,1,1); ui = Sfun{1}; % streamwise velocity vi = Sfun{2}; % wall-normal velocity % discretized values for plotting uvec(:,n) = ui(yd,1); vvec(:,n) = vi(yd,1); end % Getting physical fields of u and v kx = abs(kxval(1)); xval = linspace(0, 4*pi/kx, 100); % streamwise coordinate Up = zeros(N,length(xval)); % physical value of u Vp = zeros(N,length(xval)); % physical value of v for indx = 1:length(xval) x = xval(indx); for n = 1:2 kx = kxval(n); Up(:,indx) = Up(:,indx) + uvec(:,n)*exp(1i*kx*x); Vp(:,indx) = Vp(:,indx) + vvec(:,n)*exp(1i*kx*x); end end Up = real(Up); Vp = real(Vp); % only real part exists % Plotting the most amplified streamwise velocity structures pcolor(xval,yd,Up); shading interp; cb = colorbar('vert'); xlab = xlabel('x', 'interpreter', 'tex'); ylab = ylabel('y', 'interpreter', 'tex'); set(xlab, 'FontName', 'cmmi10', 'FontSize', 20); set(ylab, 'FontName', 'cmmi10', 'FontSize', 20); h = get(gcf,'CurrentAxes'); set(h,'FontName','cmr10','FontSize',15,'xscale','lin','yscale','lin'); set(cb, 'FontName', 'cmr10', 'FontSize', 15);
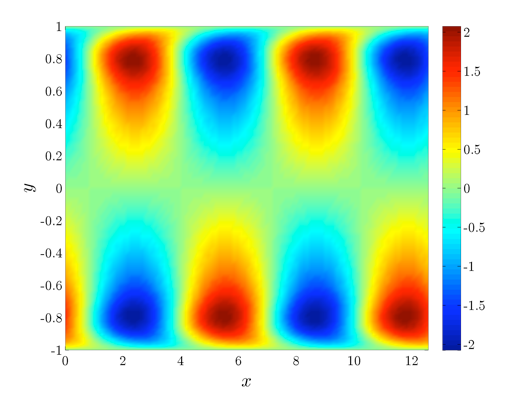 |
Plot the most amplified wall-normal velocity structures.
pcolor(xval,yd,Vp); shading interp; cb = colorbar('vert'); xlab = xlabel('x', 'interpreter', 'tex'); ylab = ylabel('y', 'interpreter', 'tex'); set(xlab, 'FontName', 'cmmi10', 'FontSize', 20); set(ylab, 'FontName', 'cmmi10', 'FontSize', 20); h = get(gcf,'CurrentAxes'); set(h,'FontName','cmr10','FontSize',15,'xscale','lin','yscale','lin'); set(cb, 'FontName', 'cmr10', 'FontSize', 15);
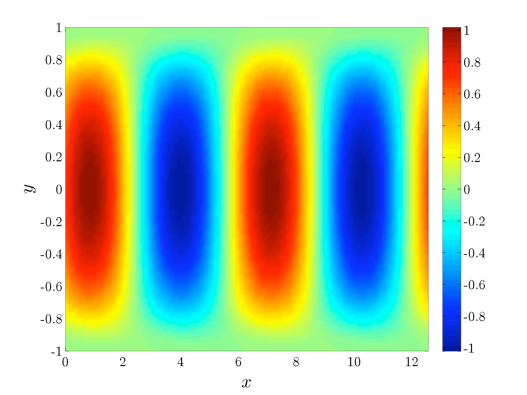 |