X = output.X;
Z = output.Z;
[Af,Bf,Cf,Df] = linfilter(A,X,Z);
[mb, nb]=size(Bf);
Xsqrt = sqrtm(X);
cvx_clear
cvx_begin
variable K(nb,mb);
variable Rho(nb,nb)
minimize norm(K*Xsqrt,'fro')
subject to
(Af-Bf*K)*X + X*(Af-Bf*K)' + Bf*Rho*Bf' == 0;
Rho >= 0;
cvx_end
Af1 = Af - Bf*K;
Af_ext = Af1;
Bf_ext = Bf;
Cf_ext = -K;
Df_ext = Df;
[l1, l2] = size(Bf_ext);
m = l2;
clear tsim x yout covY covYea varUcea covYall
Snum = 20;
Ts = 0.01;
t = 0:Ts:800;
for n = 1:Snum
[tsim(n,:),x(n,:,:),yout(n,:,:)] = sim('sim_mdl',t,simset('Decimation',100,'OutputPoints','specified'));
[n]
end
clear covY covYea varUcea covYall
ynew = x;
tnew = tsim;
[yl1, yl2, yl3] = size(ynew);
[tl1, tl2] = size(tnew);
tstart = 0;
covY = zeros(Snum,tl2-tstart,yl3,yl3);
[a1, a2, a3, a4] = size(covY);
for i = 1:Snum
for n = 1:a2
covY(i,n,:,:) = squeeze(ynew(i,n+tstart,:))*squeeze(ynew(i,n+tstart,:))';
end
[i]
end
covYea = zeros(Snum,a2,2*N,2*N);
varUcea = zeros(Snum,a2);
for i = 1:Snum
for n = 1:a2
covYea(i,n,:,:) = squeeze(sum(covY(i,1:n,:,:),2)/n);
varUcea(i,n) = trace(squeeze(covYea(i,n,:,:)));
end
[i]
end
covYall = squeeze(sum(covYea,1))/Snum;
varUc = zeros(a2,1);
for n = 1:a2
varUc(n) = trace(squeeze(covYall(n,:,:)));
end
Yeval = squeeze(covYall(end,:,:));
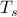 is the sampling period and
is the sampling period and 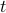 is the time vector. After running the simulations, the script averages over output measurements and computes one-point and two-point correlations. This allows the user to verify the modeling procedure by comparing the computed statistics with the available data in optimization problem (CC).
is the time vector. After running the simulations, the script averages over output measurements and computes one-point and two-point correlations. This allows the user to verify the modeling procedure by comparing the computed statistics with the available data in optimization problem (CC).