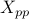Mass-spring-damper system
 |
For a stochastically-forced mass-spring-damper system with 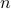 masses on a line with state-space representation
masses on a line with state-space representation
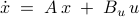
the state vector is determined by ![x = [,p^T, ~, v^T ,]^T](eqs/230197834083287441-130.png) and contains the position and velocity of all masses. The state and input matrices are
and contains the position and velocity of all masses. The state and input matrices are
![A ;=; left[ begin{array}{cc} O & I -T & -I end{array} right],~~~~ B_u ;=; left[ begin{array}{c} O I end{array} right]](eqs/2897887909991261812-130.png)
where 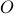 and
and 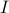 are zero and identity matrices of suitable sizes, and
are zero and identity matrices of suitable sizes, and 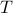 is a symmetric tridiagonal Toeplitz matrix with
is a symmetric tridiagonal Toeplitz matrix with 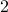 on the main diagonal and
on the main diagonal and 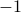 on the first upper and lower sub-diagonals. Stochastic disturbances are generated by a low-pass filter
on the first upper and lower sub-diagonals. Stochastic disturbances are generated by a low-pass filter
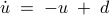
where 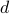 represents a zero-mean unit variance white process. The steady-state covariance of the of the stochastically-forced mass-spring-damper system can be extracted from
the steady-state covariance of the cascade of filter and system dynamics, and is partitioned as
represents a zero-mean unit variance white process. The steady-state covariance of the of the stochastically-forced mass-spring-damper system can be extracted from
the steady-state covariance of the cascade of filter and system dynamics, and is partitioned as
![Sigma_{xx} ;=; left[ begin{array}{cc} Sigma_{pp} & Sigma_{pv} Sigma_{vp} & Sigma_{vv} end{array} right]](eqs/5576808532550153589-130.png)
 |
We assume knowledge of one-point correlations of the position and velocity of |
Performance comparison
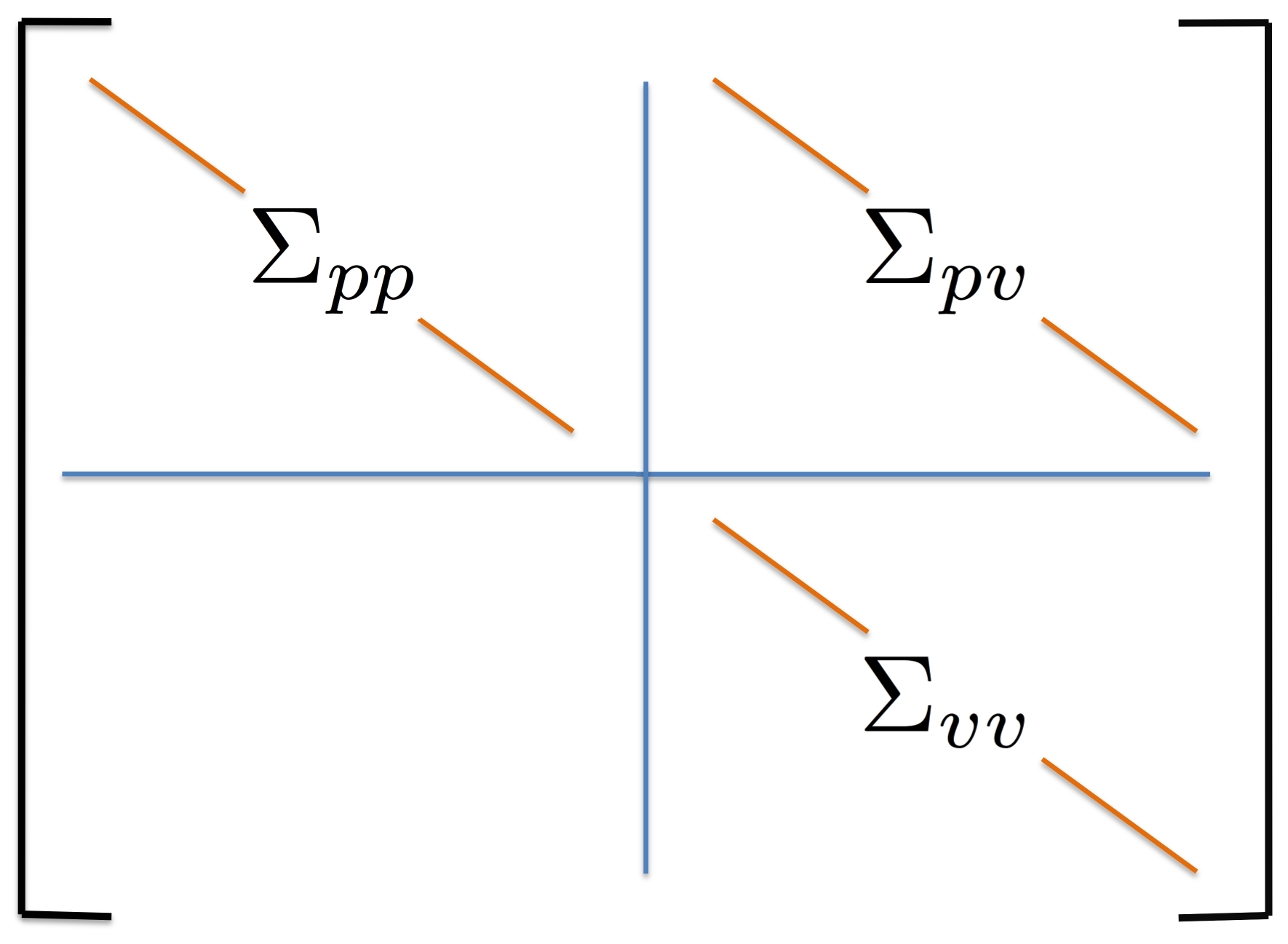
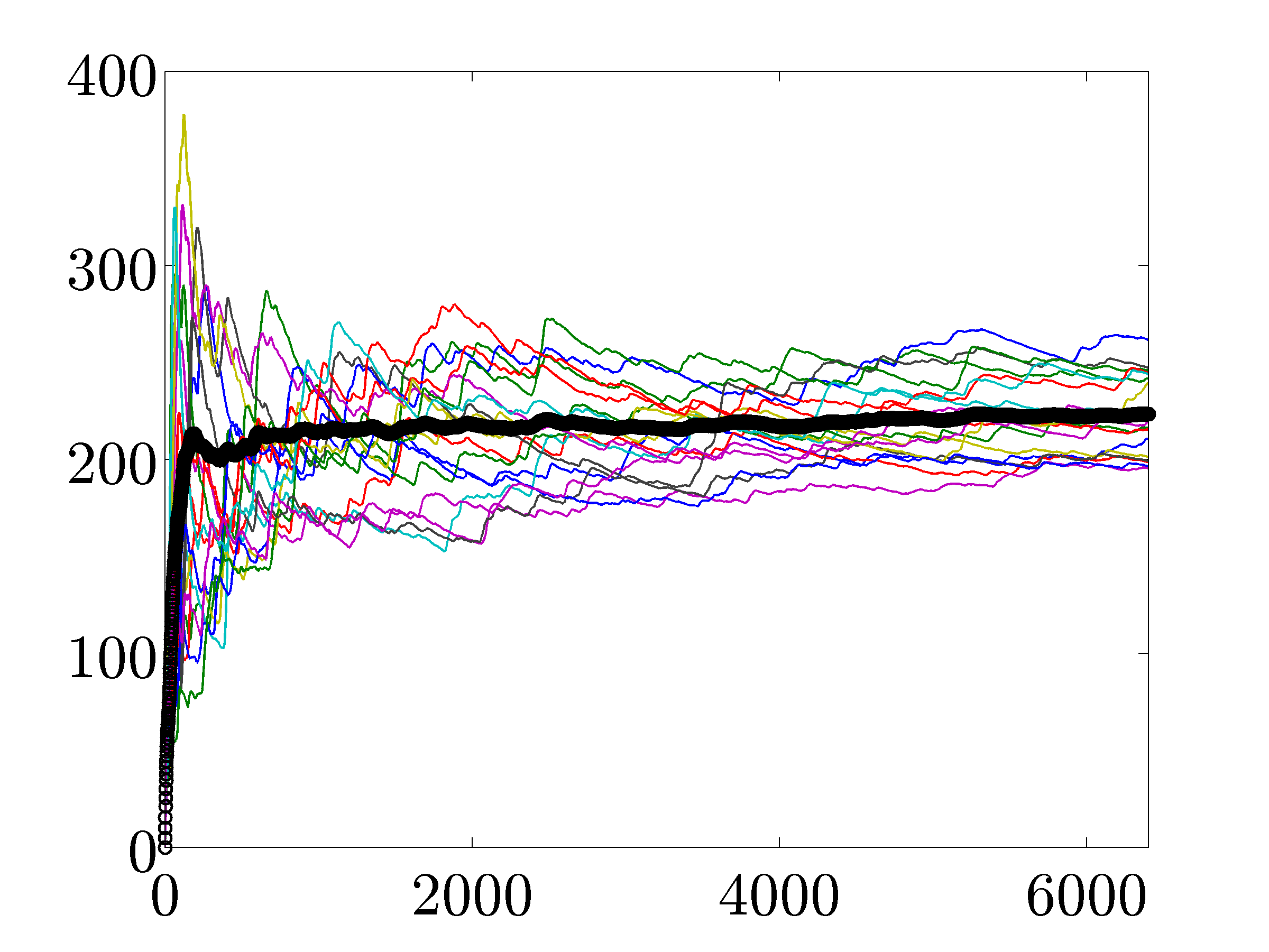
The following table compares solve times of CVX and the customized algorithms discussed in the paper. Each method stops when an iterate achieves a certain distance from optimality, i.e., 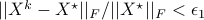 and
and 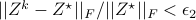 . The choice of
. The choice of 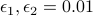 , guarantees that the primal objective is within
, guarantees that the primal objective is within 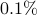 of
of 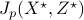 . For
. For 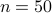 and
and 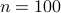 , CVX ran out of memory. Clearly, for large problems, AMA with BB step-size initialization significantly outperforms both regular AMA and ADMM.
, CVX ran out of memory. Clearly, for large problems, AMA with BB step-size initialization significantly outperforms both regular AMA and ADMM.
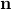 |  |  |  |  | ||||
 | 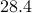 | 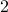 | 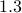 | 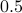 | ||||
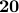 | 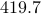 | 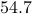 | 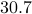 | 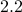 | ||||
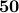 |  | 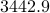 | 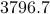 | 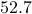 | ||||
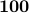 |  | 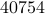 | 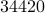 | 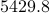
|
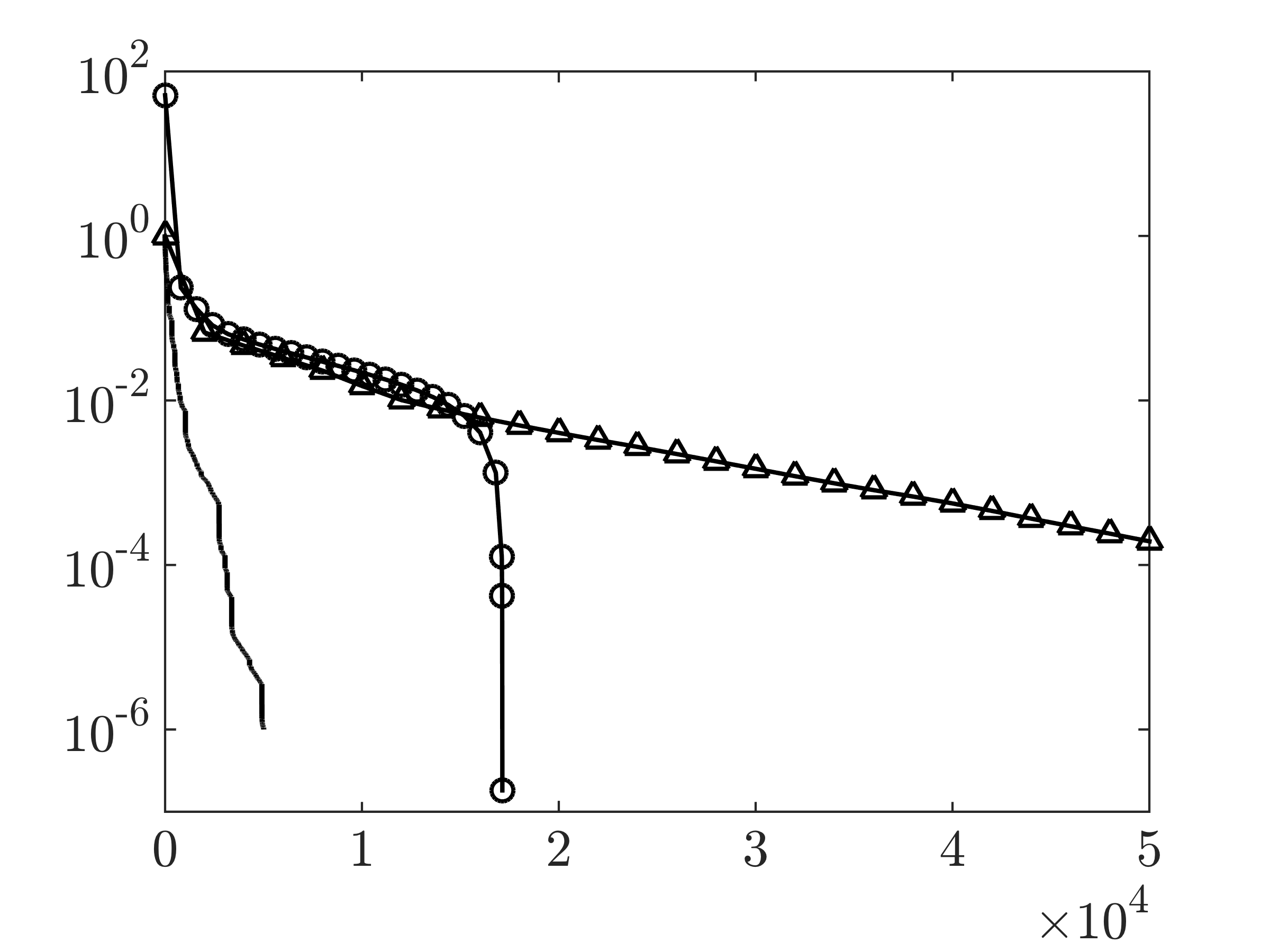 |
Convergence curves showing the performance of the customized AMA |
Quality of completion and verification in linear stochastic simulations
For 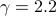 , the spectrum of
, the spectrum of 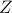 contains
contains 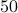 positive and
positive and 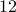 negative eigenvalues. Based on Proposition
negative eigenvalues. Based on Proposition 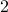 of the paper,
of the paper, 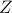 can be decomposed into
can be decomposed into 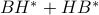 , where
, where 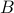 has
has  independent columns. In other words, the identified
independent columns. In other words, the identified 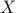 can be explained by driving the state-space model with
can be explained by driving the state-space model with 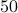 stochastic inputs
stochastic inputs 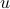 . Based on this, we construct the optimal filter that generates the suitable stochastic input and conduct linear stochastic simulations of the filter dynamics with zero-mean unit variance input to validate our modeling approach.
. Based on this, we construct the optimal filter that generates the suitable stochastic input and conduct linear stochastic simulations of the filter dynamics with zero-mean unit variance input to validate our modeling approach.
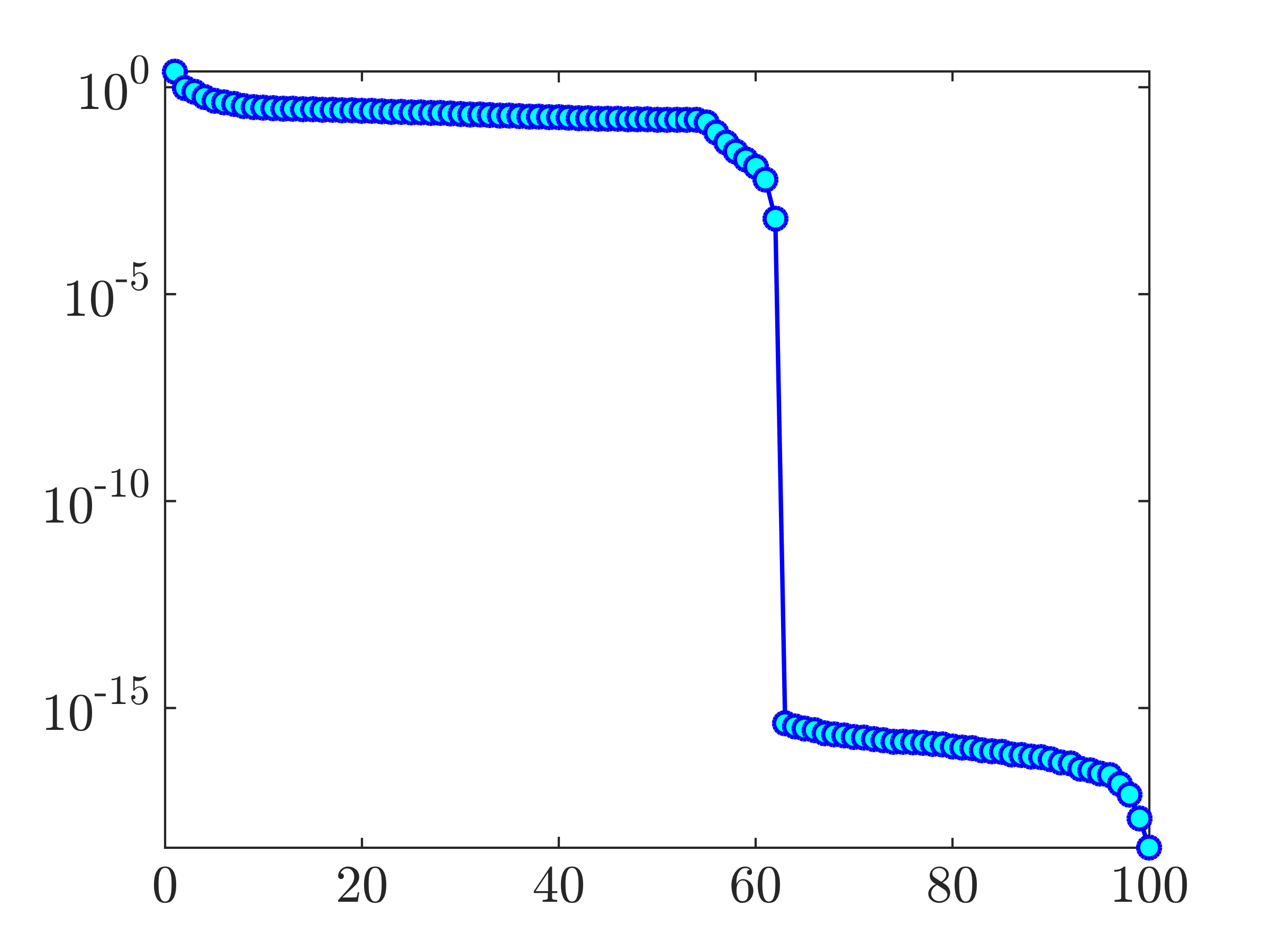 |
For |
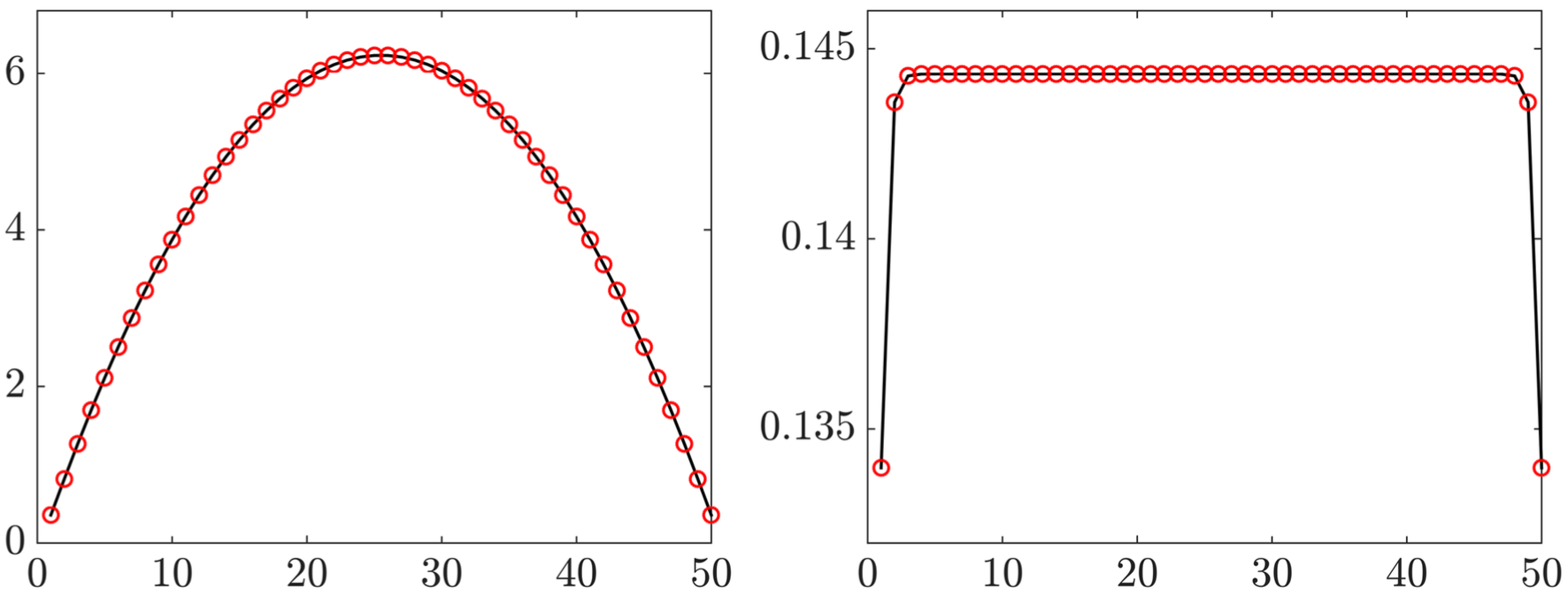 |
Diagonals of position (left) and velocity |
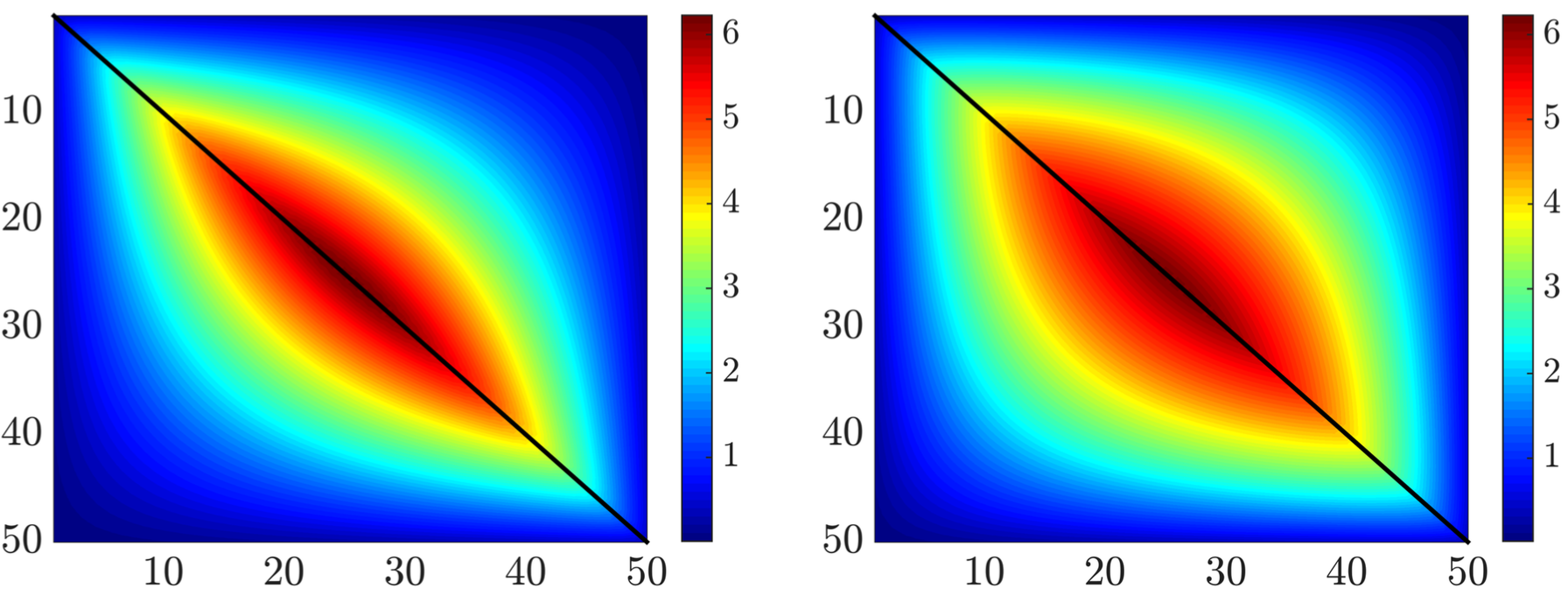 |
The true covariance |
 |
Time evolution of the variance of the mass-spring-damper system's |
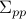 ,
, 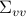 , and
, and 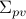 , which are
, which are 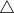 ) BB step-size initialization and ADMM (
) BB step-size initialization and ADMM ( )
) 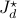 is the optimal dual objective.
is the optimal dual objective.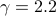 , the matrix
, the matrix 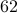 of them being nonzero.
of them being nonzero.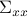 and
and