% A 2D lattice example for the noise-corrupted leader-selection problem. % % form the incidence matrix and graph Laplacian matrix for 2D lattice % % number of nodes for the N x N 2D lattice n = 81; N = sqrt(n); % compute the number of edges ne = 0.5*( 2*4 + (N-2)*3*4 + (N-2)^2*4 ); % form the index set of edges idx = zeros(2,ne); % evaluate the indices for those edges on the rows of the grid for i = 1:N idx(1,(N-1)*(i-1)+1:(N-1)*i) = N*(i-1)+1:N*(i-1)+(N-1); idx(2,(N-1)*(i-1)+1:(N-1)*i) = N*(i-1)+2:N*(i-1)+N; end % evaluate the indices for those edges on the columns of the grid for i = 1:N idx(1,ne/2+ ((N-1)*(i-1)+1:(N-1)*i) ) = i:N:(i+(N-2)*N); idx(2,ne/2+ ((N-1)*(i-1)+1:(N-1)*i) ) = (i:N:(i+(N-2)*N))+N; end % form the incidence matrix Eg of the 2D lattice Eg = incmat(idx); % form the graph Laplacian L = Eg*Eg'; % kappa is taken as the diagonal of L kappa = diag(L); % Start solving the leader selection problem % % choose the number of leaders kval = 1:1:40; % pre-allocate memory for data collection Jlow = zeros(size(kval)); Jup = zeros(size(kval)); LSgreed = zeros(n,length(kval)); for i = 1:length(kval) Nl = kval(i); flag = 1; % for the noise-corrupted leader selection formulation [Jlow(i),Jup(i),LSgreed(:,i)] = leaders(L,Nl,kappa,flag); end
A 2D lattice
 |
We consider the noise-corrupted leader selection problem for a 2D regular lattice with |
Matlab code
Computational results
Download Matlab code lattice_example.m to reproduce these figures.
Performance bounds
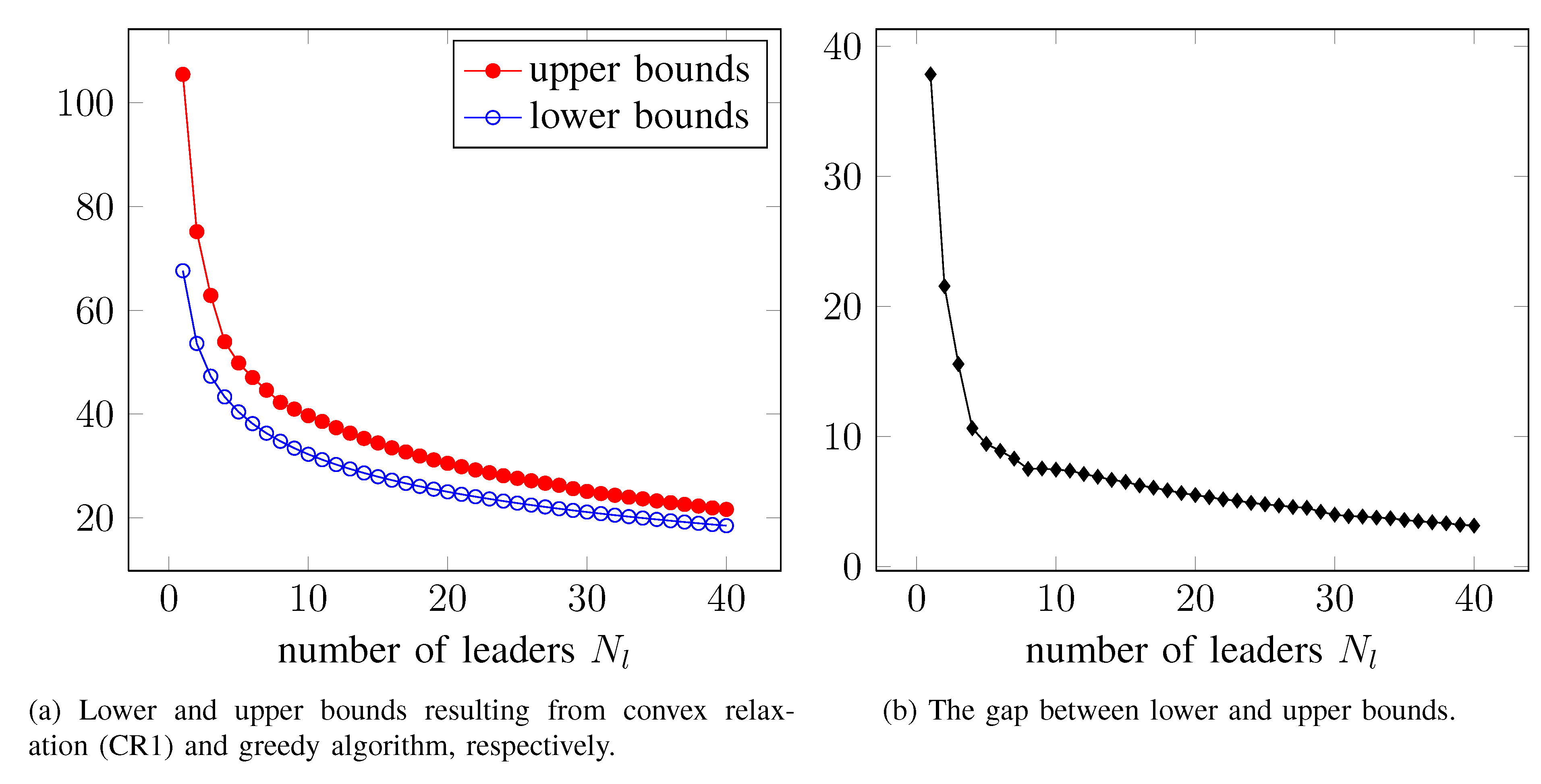 |
Bounds on the global optimal value of the noise-corrupted leader selection problem
 for the 2D lattice example.
for the 2D lattice example.
Selection of leaders
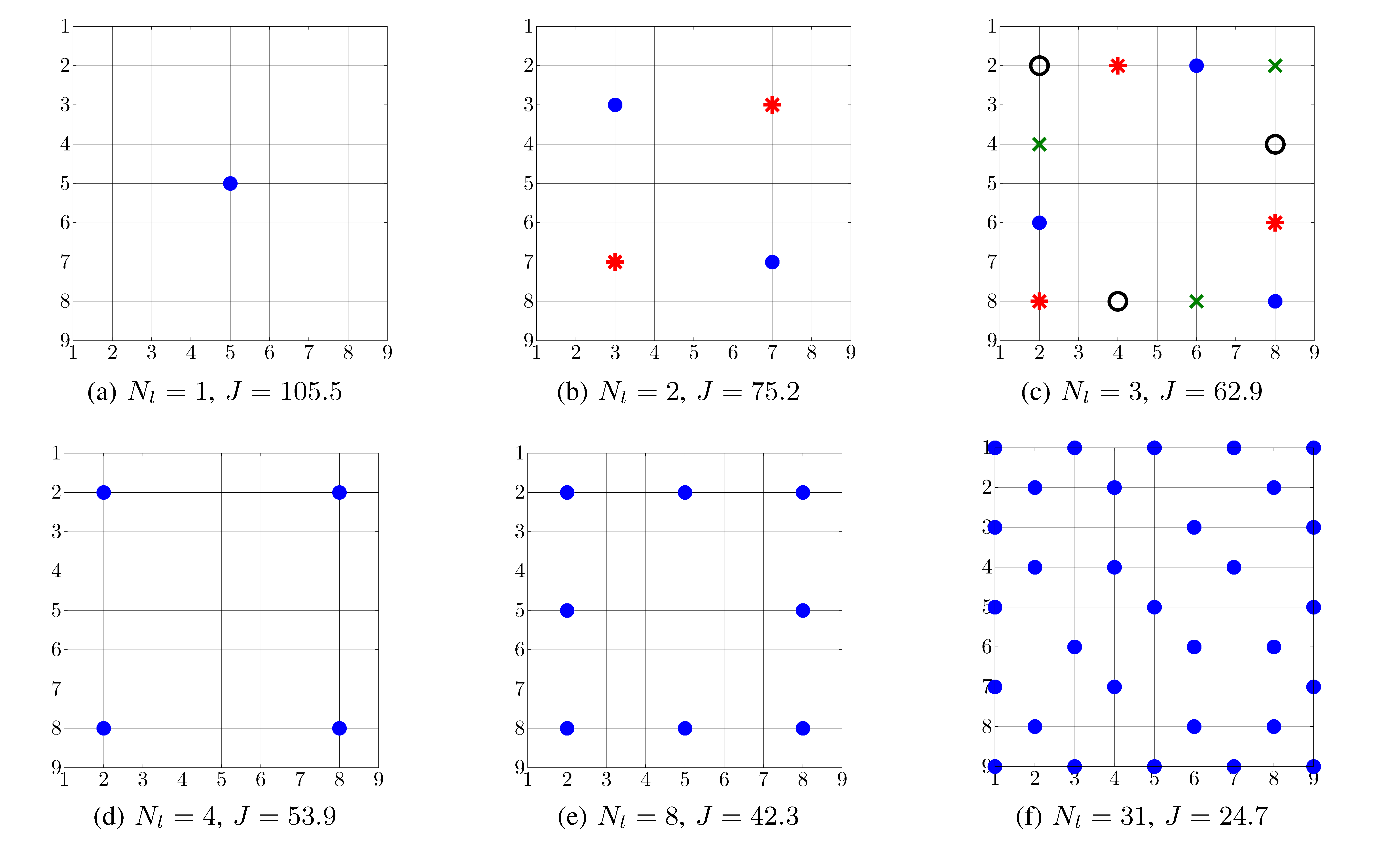 |
Selection of noise-corrupted leaders ( ) obtained using
greedy algorithm (i.e., one-leader-at-a-time algorithm followed by the swap procedure)
for the 2D lattice example.
) obtained using
greedy algorithm (i.e., one-leader-at-a-time algorithm followed by the swap procedure)
for the 2D lattice example.
For 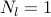 , the center node
, the center node 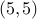 provides the optimal
selection of a single leader. As
provides the optimal
selection of a single leader. As 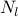 increases, nodes away from the center
node are selected; for example, for
increases, nodes away from the center
node are selected; for example, for 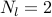 , nodes
, nodes 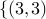 ,
, 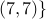 are
selected and for
are
selected and for 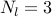 , nodes
, nodes 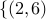 ,
, 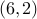 ,
, 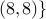 are selected.
Selection of nodes farther away from the center becomes more significant for
are selected.
Selection of nodes farther away from the center becomes more significant for
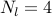 and
and 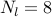 .
.
The selection of leaders exhibits symmetry with respect to the center
of the lattice. For example, in Fig. (b), the leaders at 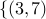 ,
, 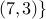 denoted by
(
denoted by
( ) provide the same objective function
) provide the same objective function 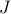 as leaders denoted by (
as leaders denoted by ( ). Similarly,
in Fig. (c), the four selections of three leaders denoted by (
). Similarly,
in Fig. (c), the four selections of three leaders denoted by ( ), (
), ( ),
(
),
(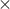 ), and (
), and ( ) all provide the same performance
) all provide the same performance 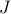 .
.
Also note that when 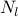 is large, almost uniform spacing between leaders is
observed; see Fig. (f). This is in contrast to the random network example where boundary nodes were selected when the number
of leaders is large.
is large, almost uniform spacing between leaders is
observed; see Fig. (f). This is in contrast to the random network example where boundary nodes were selected when the number
of leaders is large.
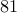 nodes.
nodes.