Spring 2015 MnDRIVE Seminar Series
 |
Izchak Lewkowicz,
Ben-Gurion University of the Negev
|
Abstract
Convex Invertible Cones (CICs in short) of matrices or of rational functions are sets which are closed under positive scaling summation and inversion (whenever the matrix is non-singular). In the context of driving point impedance of R-L-C electrical circuits, scaling means transformer ratio, summation takes the form series connection and inversion is interpreted is impedance/admittance duality. Although not well studied, CICs appear in numerous places. In this talk we offer a sample list, and make interconnections among the items.
The set of all Linear Time-Invariant systems sharing common quadratic Lyapunov functions is a maximal CIC of matrices.
The set of rational positive real rational functions is a maximal CIC of rational functions.
The set of realizations of
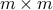 -valued positive real rational
functions of Mc-Millan degree up to
-valued positive real rational
functions of Mc-Millan degree up to 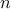 , is a maximal CIC of matrices.
, is a maximal CIC of matrices.
The structure of singly generated CIC is analogous to Nevannlina-Pick interpolation problem.
Arbitrary interconnection of multiple feedback loops forms a CIC.
The actual list is much longer and as time permits, generalizations will be given. Part of the motivation is to open the door to more research in this area. For example, from control applications point of view, to exploit classical electrical circuits synthesis techniques, e.g. Brune, Darlington etc. to the design of complicated multiple feedback loop system. From mathematical analysis, to extend classical Nevanlinna-Pick interpolation to rational functions of several non-commuting variable with a certain positivity.