Fall 2014 MnDRIVE Seminar Series
 |
Joost Veenman,
University of Stuttgart
|
Abstract
In this talk we consider a general framework for the systematic synthesis
of robust gain-scheduling controllers by convex optimization techniques and
for uncertain dynamical systems described by standard linear fractional
representations. We distinguish between linear time-varying parameters,
which are assumed to be available online as scheduling parameters for the
controller, and genuine uncertainties, not necessarily time-varying,
parametric or linear, that are not available online. Under the rough
hypothesis that the control channel is not affected by the unmeasurable
uncertainties and that the properties of the uncertainties and scheduling
variables are captured by suitable families of integral quadratic
constraints (IQCs), it will be shown that controller synthesis can be
turned into a genuine semi-definite program. This design framework is shown
to encompass a rich class of concrete scenarios, such as robust estimator
or observer design, robust feed-forward control, generalized 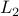 -synthesis,
gain-scheduling output-feedback control with uncertain performance weights
and robust control with unstable weights, among others.
-synthesis,
gain-scheduling output-feedback control with uncertain performance weights
and robust control with unstable weights, among others.
Biosketch
Joost Veenman received the MSc degree in mechanical engineering in 2008 from Delft University of Technology, Delft, The Netherlands. From September 2008 to May 2010 he stayed in Delft and worked as a researcher within the Delft Center for Systems and Control (DCSC). During this period he was part of the LPVMAD project; a joint project of the European Space Agency (ESA), Deimos Space, the Delft University of Technology and the University of Leicester. The project had as main goal to develop and validate Modeling, Analysis and Design (MAD) tools for Linear Parameter Varying (LPV) systems (hence the name LPVMAD) with a re-entry vehicle as benchmark study-case. After a successful completion of the project he moved to Germany in May 2010. He is currently affiliated with the chair of Mathematical Systems Theory (Prof. Dr. Carsten W. Scherer, Department of Mathematics, University of Stuttgart, Germany) and is working towards his PhD degree. His main research interests are robustness analysis, robust (gain-scheduling) control, and linear matrix inequality (LMI) techniques.